
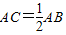 ,求证:∠B=30°,请你完成证明过程.
,求证:∠B=30°,请你完成证明过程.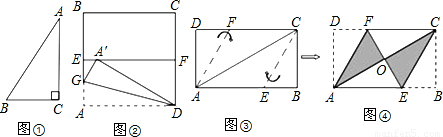
 =
= ,即可证明∠B=30°;
,即可证明∠B=30°; AC,得出∠ACD=30°,∠DAC=60°,从而求出AD的长度,根据翻折变换的性质可得出∠DAF=∠FAO=30°,在Rt△ADF中求出DF,继而得出FO,同理可求出EO,再由EF=EO+FO,即可得出答案.
AC,得出∠ACD=30°,∠DAC=60°,从而求出AD的长度,根据翻折变换的性质可得出∠DAF=∠FAO=30°,在Rt△ADF中求出DF,继而得出FO,同理可求出EO,再由EF=EO+FO,即可得出答案.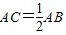 ,
,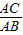 =
= ,
, ×边长=1,
×边长=1,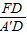 =
= ,
,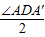 =
=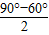 =15°,
=15°,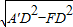 =
=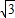 ,
, ,
,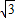 );
);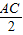 ,
, =tan30°,
=tan30°, =2
=2 ,
, ∠DAO=
∠DAO=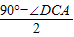 =30°,
=30°, =tan30°=
=tan30°= ,
,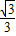 AD=2,
AD=2,

科目:初中数学 来源: 题型:
| A、50 | B、50或40 | C、50或40或30 | D、50或30或20 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| A、-7xy | B、7xy |
| C、-xy | D、xy |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
 +y2 阴影的地方被钢笔水弄污了,那么空格中的一项是( )
+y2 阴影的地方被钢笔水弄污了,那么空格中的一项是( )| A、-7xy | B、+7xy |
| C、-xy | D、+xy |
查看答案和解析>>
科目:初中数学 来源: 题型:
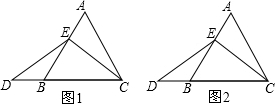 (2013•许昌一模)某次数学课上,老师出示了一道题,如图1,在边长为4等边三角形ABC中,点E在AB上.
(2013•许昌一模)某次数学课上,老师出示了一道题,如图1,在边长为4等边三角形ABC中,点E在AB上.| AE |
| AB |
| 1 |
| 3 |
| 16 |
| 3 |
| 16 |
| 3 |
| AE |
| AB |
| 1 |
| n |
| mn+m |
| n |
| mn+m |
| n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com