
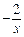 的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.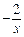 ,P点坐标为(1, 0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;
,P点坐标为(1, 0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标; 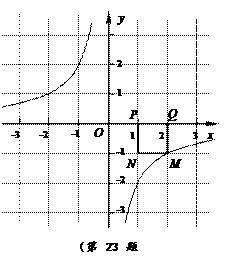
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源:不详 题型:解答题
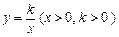 的图象经过点A(1, 2),B(m ,n)(m>1),过点B作y轴的垂线,垂足为C.
的图象经过点A(1, 2),B(m ,n)(m>1),过点B作y轴的垂线,垂足为C.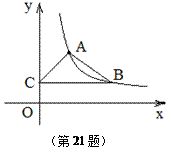
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 反比例函数
反比例函数 在第一象限图像上的一点,点A1的坐标为(2,0).
在第一象限图像上的一点,点A1的坐标为(2,0).
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 ,AB=AC=2,点A在直线
,AB=AC=2,点A在直线 上,其中点A的横坐标为1,且AB∥
上,其中点A的横坐标为1,且AB∥ 轴,AC∥
轴,AC∥ 轴,若双曲线
轴,若双曲线
 与△
与△ 有交点,则k的取值范围是 .
有交点,则k的取值范围是 .
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| k |
| x |
| 1 |
| a |
A.(-
| B.(
| C.(-b,
| D.(b,-
|
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| 2 |
| x |
| A.1 | B.2 | C.4 | D.不能确定 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com