(1)证明:∵AB是直径,
∴∠ACB=90°.
∴∠CAB+∠ABC=90°.
∵∠MAC=∠ABC,
∴∠MAC+∠CAB=90°.
即MA⊥AB.
∴MN是半圆的切线.
(2)证明:
证法1:∵D是弧AC的中点,
∴∠DBC=∠2.
∵AB是直径,
∴∠CBG+∠CGB=90°.
∵DE⊥AB,
∴∠FDG+∠2=90°.
∵∠DBC=∠2,
∴∠FDG=∠CGB=∠FGD.
∴FD=FG.

证法2:连接AD,则∠1=∠2,
∵AB是直径,
∴∠ADB=90°.
∴∠1+∠DGF=90°.
又∵DE⊥AB,
∴∠2+∠FDG=90°.
∴∠FDG=∠FGD.
∴FD=FG.
(3)解:解法1:过点F作FH⊥DG于H,
又∵DF=FG,
∴S
△FGH=

S
△DFG=

×4.5=

.
∵AB是直径,FH⊥DG,
∴∠C=∠FHG=90°.
∵∠HGF=∠CGB,
∴△FGH∽△BGC.
∴

.
∴S
△BCG=

=16.
解法2:∵∠ADB=90°,DE⊥AB,
∴∠3=∠2.
∵∠1=∠2,
∴∠1=∠3.
∴AF=DF=FG.
∴S
△ADG=9.
∵∠ADG=∠BCG,∠DGA=∠CGB.
∴△ADG∽△BCG.
∴

.
∴S
△BCG=

.
解法3:连接AD,过点F作FH⊥DG于H.
∵S
FDG=

DG×FH=

×3FH=4.5,
∴FH=3.
∵H是DG的中点,FH∥AD,
∴AD=2FH=6
∴S
△ADG=

.
∵∠ADG=∠BCG,∠DGA=∠CGB.
∴△ADG∽△BCG.
∵DG=3,GC=4,
∴

=(
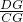
)
2,
∴

=(

)
2,
∴S
△BCG=16.
分析:(1)要证MN是⊙O的切线,只需证明MA⊥AB即可,易得∠MAC+∠CAB=90°,即MA⊥AB;故可得证.
(2)连接AD,则∠1=∠2,进而可得∠1+∠DGF=90°,故∠FDG=∠FGD,即FD=FG.
(3)求△BCG的面积,只需证得△FGH∽△BGC,再根据相似三角形的性质,求得△BCG的面积.
点评:本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

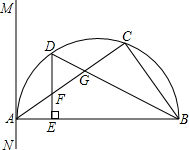 如图,△ABC内接于半圆,AB为直径,过点A作直线MN,若∠MAC=∠ABC.
如图,△ABC内接于半圆,AB为直径,过点A作直线MN,若∠MAC=∠ABC. 证法2:连接AD,则∠1=∠2,
证法2:连接AD,则∠1=∠2, S△DFG=
S△DFG= ×4.5=
×4.5= .
. .
. =16.
=16. .
. .
. DG×FH=
DG×FH= ×3FH=4.5,
×3FH=4.5, .
. =(
=(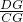 )2,
)2, =(
=( )2,
)2,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.
21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.