
分析 (1)由轿车可行驶的总路程S(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系,可设S=$\frac{k}{a}$,再将a=0.1,S=800代入S=$\frac{k}{a}$,即可求得k的值,从而确定解析式;
(2)将a=0.08代入求得的函数的解析式即可求得S的值.
解答 解:(1)由题意可设S=$\frac{k}{a}$,
∵a=0.1,S=800,
∴800=$\frac{k}{0.1}$,
解得:k=80,
所以函数关系式为:S=$\frac{80}{a}$;
(2)将a=0.08代入S=$\frac{80}{a}$,
得:S=$\frac{80}{0.08}$=1000,
故该轿车可以行驶1000千米.
点评 本题考查了反比例函数的应用,解题的关键是从实际问题中抽象出反比例函数模型,然后利用待定系数法求出关系式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连结CN.若BM=1,BC=5,则MN的长为( )
如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连结CN.若BM=1,BC=5,则MN的长为( )| A. | 2 | B. | 4 | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠ABC=90° | B. | AC=BD | C. | AC2=AB2+BC2 | D. | AC⊥BD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
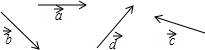 如图,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,求作:
如图,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,求作:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com