
若a,b,c是直角三角形的三条边长,斜边c上的高的长是h,给出下列结论:
①以a2,b2,c2的长为边的三条线段能组成一个三角形;②以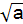 ,
,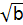 ,
, 的长为边的三条线段能组成一个三角形;③以a+b,c+h,h的长为边的三条线段能组成直角三角形;④以
的长为边的三条线段能组成一个三角形;③以a+b,c+h,h的长为边的三条线段能组成直角三角形;④以 ,
, ,
, 的长为边的三条线段能组成直角三角形.
的长为边的三条线段能组成直角三角形.
其中所有正确结论的序号为 .
①直角三角形的三条边满足勾股定理a2+b2=c2,因而以a2,b2,c2的长为边的三条线段不能满足两边之和大于第三边,故不能组成一个三角形,故错误;②直角三角形的三 边有a+b>c(a,b,c中c最大),而在
边有a+b>c(a,b,c中c最大),而在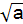 ,
,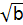 ,
, 三个数中
三个数中 最大,如果能组成一个三角形,则有
最大,如果能组成一个三角形,则有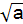 +
+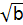 >
> 成立,即(
成立,即(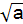 +
+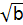 )2>(
)2>( )2,即a+b+2
)2,即a+b+2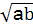 >c(由a+b>c),则不等式成立,从而满足两边之和大于第三边,则以
>c(由a+b>c),则不等式成立,从而满足两边之和大于第三边,则以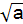 ,
,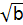 ,
, 的长为边的三条线段能组成一个三角形,故正确;③a+b,c+h,h这三个数
的长为边的三条线段能组成一个三角形,故正确;③a+b,c+h,h这三个数 中c+h一定最大,(a+b)2+h2=a2+b2+2ab+h2,(c+h)2=c2+h2+2ch,
中c+h一定最大,(a+b)2+h2=a2+b2+2ab+h2,(c+h)2=c2+h2+2ch,
又∵2ab=2ch=4S△ABC,∴(a+b)2+h2=(c+h)2,根据勾股定理的逆定理即以a+b,c+h,h的长为边的三条线段能组成直角三角形,故正确;④假设a =3,b=4,c=5,则
=3,b=4,c=5,则 ,
, ,
, 的长为
的长为 ,
, ,
, ,以这三个数的长为边的三条线段不能组成直角三角形,故错误.
,以这三个数的长为边的三条线段不能组成直角三角形,故错误.
答案:②③


科目:初中数学 来源: 题型:
如图,平行线AB、CD被直线AE所截.
(1)从∠1=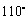 ,则可知道∠2= 度,
,则可知道∠2= 度,
 根据 ;
根据 ;
(2)从∠1=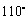 ,则可知道∠3= 度,
,则可知道∠3= 度,
根据 ;
(3)从∠1=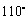 ,则可知道∠4= 度,
,则可知道∠4= 度,
根据 .
查看答案和解析>>
科目:初中数学 来源: 题型:
设边长为3的正方形的对角线长为a,下列关 于a的四种说法:①a是无理数;②a可以用数轴上的一个点来表示;③3<a<4;④a是18的算术平方根.其中,所有正确说法的序号是( )
于a的四种说法:①a是无理数;②a可以用数轴上的一个点来表示;③3<a<4;④a是18的算术平方根.其中,所有正确说法的序号是( )
A.①④ B.②③
C.①② ④ D.①③④
④ D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
勾股定理揭示了直角三角形三边之间的关系,其中蕴含着丰富的科学知识和人文价值.如图所示,是一棵由正方形和含30°角的直角三角形按一定规律长成的勾股树,树主干自下而上第一个正方形和第一个直角三角形的面积之和为S1,第二个正方形和第二个直角三角形的面积之和为S2,…,第n个正方形和第n个直角三角形的面积之和为Sn.设第一个正方形的边长为1.
请解答下列问题:
(1)S1= .
(2)通过探究,用含n的式子表示Sn,则Sn= .

查看答案和解析>>
科目:初中数学 来源: 题型:
在如图所示的三个函数图象中,有两个函数图象能近似地刻画如下a,b两个情境:

情境a:小芳离开家不久,发现把作业本忘在家里,于是返回了家里找到了作业本再去学校;
情境b:小芳从家出发,走了一段路程后,为了赶时间,以更快的 速度
速度 前进.
前进.
(1)情境a,b所对应的函数图象分别是 , (填写序号).
(2)请你为剩下的函数图象写出一个适合的情境.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,活动衣帽架由三个菱形组成,利用 四边形的不稳定性,调整菱形的内角α,使衣帽架拉伸或收缩.当菱形的边长为18c
四边形的不稳定性,调整菱形的内角α,使衣帽架拉伸或收缩.当菱形的边长为18c m,α=120°时,A,B两点的距离为
m,α=120°时,A,B两点的距离为
cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com