
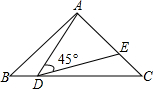
 在Rt△ABC中,∠BAC=90°,AB=AC=10,点D在BC所在的直线上运动,作∠ADE=45°(A,D,E按逆时针方向).如图,若点D在线段BC上运动,DE交AC于E.
在Rt△ABC中,∠BAC=90°,AB=AC=10,点D在BC所在的直线上运动,作∠ADE=45°(A,D,E按逆时针方向).如图,若点D在线段BC上运动,DE交AC于E.| 2 |
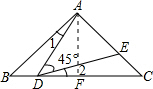 解:(1)如图,∵∠BAC=90°,AB=AC,
解:(1)如图,∵∠BAC=90°,AB=AC,| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com