
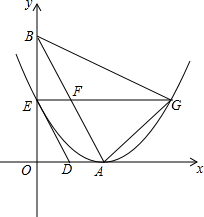
 ��ͼ��ֱ��y=-$\sqrt{3}$x+2$\sqrt{3}$��x�ᣬy��ֱ��ڵ�A����B��������D��E�ֱ�ӵ�A����Bͬʱ�������O�˶����˶�����Oֹͣ�����˶��ٶȷֱ���1����λ����/���$\sqrt{3}$����λ����/�룬���˶�ʱ��Ϊt�룬�Ե�AΪ����������߾�����E������E��x���ƽ���ߣ��������ߵ���һ������Ϊ��G����AB�ཻ�ڵ�F��
��ͼ��ֱ��y=-$\sqrt{3}$x+2$\sqrt{3}$��x�ᣬy��ֱ��ڵ�A����B��������D��E�ֱ�ӵ�A����Bͬʱ�������O�˶����˶�����Oֹͣ�����˶��ٶȷֱ���1����λ����/���$\sqrt{3}$����λ����/�룬���˶�ʱ��Ϊt�룬�Ե�AΪ����������߾�����E������E��x���ƽ���ߣ��������ߵ���һ������Ϊ��G����AB�ཻ�ڵ�F������ ��1����ֱ��y=-$\sqrt{3}$x+2$\sqrt{3}$�У��ֱ���y=0��x=0���������A��B�������ꣻ
��2����OA��OB�ij�����á�ABO=30�㣬��t�ɱ�ʾ��BE��EF����BF�ij����ɹ��ɶ��������AB�ij����Ӷ�����t��ʾ��AF�ij���
��3���������ε����ʿ����t��ֵ��������AF=AG�ij����ɵõ�$\frac{AF}{AG}$=$\frac{AG}{AB}$�����ж���AFG���AGB���ƣ�
��4������AGFΪֱ��������ʱ����������ֻ֪���ǡ�FAG=90�㣬�֡�AFG=��OAF=60�㣬�ɣ�2����֪AF=4-2t��EF=t�����ɶ��κ����ĶԳ��Կɵõ�EG=2OA=4���Ӷ������FG����Rt��AGF�У��ɵõ�����t�ķ��̣������t��ֵ����һ�������E�����꣬���ô���ϵ��������������ߵĽ���ʽ��
��� �⣺
��1����ֱ��y=-$\sqrt{3}$x+2$\sqrt{3}$�У�
��y=0�ɵ�0=-$\sqrt{3}$x+2$\sqrt{3}$�����x=2��
��x=0�ɵ�y=2$\sqrt{3}$��
��A��2��0����B��0��2$\sqrt{3}$����
��2���ɣ�1����֪OA=2��OB=2$\sqrt{3}$��
��tan��ABO=$\frac{OA}{OB}$=$\frac{\sqrt{3}}{3}$��
���ABO=30�㣬
���˶�ʱ��Ϊt�룬
��BE=$\sqrt{3}$t��
��EF��x�ᣬ
����Rt��BEF�У�EF=BE•tan��ABO=$\frac{\sqrt{3}}{3}$BE=t��BF=2EF=2t��
��Rt��ABO��OA=2��OB=2$\sqrt{3}$��
��AB=4��
��AF=4-2t��
��3�����ƣ��������£�
���ı���ADEFΪ����ʱ������EF=AF��
��t=4-2t�����t=$\frac{4}{3}$��
��AF=4-2t=4-$\frac{8}{3}$=$\frac{4}{3}$��OE=OB-BE=2$\sqrt{3}$-$\sqrt{3}$��$\frac{4}{3}$=$\frac{2\sqrt{3}}{3}$��
��ͼ����G��GH��x�ᣬ��x���ڵ�H��
���ı���OEGHΪ���Σ�
��GH=OE=$\frac{2\sqrt{3}}{3}$��
��EG��x�ᣬ�����ߵĶ���ΪA��
��OA=AH=2��
��Rt��AGH�У��ɹ��ɶ����ɵ�AG2=GH2+AH2=��$\frac{2\sqrt{3}}{3}$��2+22=$\frac{16}{3}$��
��AF•AB=$\frac{4}{3}$��4=$\frac{16}{3}$��
��AF•AB=AG2����$\frac{AF}{AG}$=$\frac{AG}{AB}$���ҡ�FAG=��GAB��
���AFG�ס�AGB��
��4�����ڣ�
��EG��x�ᣬ
���GFA=��BAO=60�㣬
��G�㲻���������ߵĶԳ����ϣ�
���FGA��90�㣬
�൱��AGFΪֱ��������ʱ�����С�FAG=90�㣬
�֡�FGA=30�㣬
��FG=2AF��
��EF=t��EG=4��
��FG=4-t����AF=4-2t��
��4-t=2��4-2t����
���t=$\frac{4}{3}$��
����t��ֵΪ$\frac{4}{3}$��ʱ����AGFΪֱ�������Σ���ʱOE=OB-BE=2$\sqrt{3}$-$\sqrt{3}$t=2$\sqrt{3}$-$\sqrt{3}$��$\frac{4}{3}$=$\frac{2\sqrt{3}}{3}$��
��E��������0��$\frac{2\sqrt{3}}{3}$����
�������ߵĶ���ΪA��
����������߽���ʽΪy=a��x-2��2��
��E���������ɵ�$\frac{2\sqrt{3}}{3}$=4a�����a=$\frac{\sqrt{3}}{6}$��
�������߽���ʽΪy=$\frac{\sqrt{3}}{6}$��x-2��2��
��y=$\frac{\sqrt{3}}{6}$x2-$\frac{2\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$��
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰֪ʶ���д���ϵ���������Ǻ����Ķ��塢���������ε��ж������ʡ����ɶ��������κ����ĶԳ��Եȣ��ڣ�2������á�ABO=30���ǽ���Ĺؼ����ڣ�3�������t��ֵ����ʾ��AG�ij����ǽ���Ĺؼ����ڣ�4�����жϳ���FAGΪֱ���ǽ����ͻ�ƿڣ����⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���ѶȽϴ�


 ֥�鿪���γ�������ϵ�д�
֥�鿪���γ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��l1��Ӧ�ĺ�������ʽΪy=2x����ֱ��l1����ƽ�ƣ�ʹ֮�ֱ���x��y�ύ�ڵ�A��B����OA=2�����߶�OB�ij�Ϊ��������
��ͼ����ƽ��ֱ������ϵ�У�ֱ��l1��Ӧ�ĺ�������ʽΪy=2x����ֱ��l1����ƽ�ƣ�ʹ֮�ֱ���x��y�ύ�ڵ�A��B����OA=2�����߶�OB�ij�Ϊ��������| A�� | 3 | B�� | 4 | C�� | 2$\sqrt{2}$ | D�� | 2$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
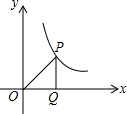 ��ͼ����P�ڷ���������y=$\frac{k}{x}$��x��0����һ����ͼ���ϣ�PQ��ֱx�ᣬ����ΪQ�����POQ�������s����ôs��k֮���������ϵ�ǣ�������
��ͼ����P�ڷ���������y=$\frac{k}{x}$��x��0����һ����ͼ���ϣ�PQ��ֱx�ᣬ����ΪQ�����POQ�������s����ôs��k֮���������ϵ�ǣ�������| A�� | $s=\frac{k}{4}$ | B�� | $s=\frac{k}{2}$ | C�� | s=k | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
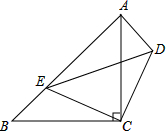 ��ͼ����ABC����CDE��Ϊ����ֱ�������Σ���ACB=��DCE=90�㣬��E��AB�ϣ���֤����CDA�ա�CEB��
��ͼ����ABC����CDE��Ϊ����ֱ�������Σ���ACB=��DCE=90�㣬��E��AB�ϣ���֤����CDA�ա�CEB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��1 | B�� | a��-1 | C�� | -1��a��1 | D�� | -1��a��0��0��a��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��0�� | B�� | ��1��-4�� | C�� | ��-1��0�� | D�� | ��-5��-1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
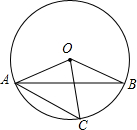 ��ͼ���ڡ�O�У�AB���ң�C��$\widehat{AB}$��һ�㣮����OAB=25�㣬��OCA=40�㣬���BOC�Ĵ�СΪ30�ȣ�
��ͼ���ڡ�O�У�AB���ң�C��$\widehat{AB}$��һ�㣮����OAB=25�㣬��OCA=40�㣬���BOC�Ĵ�СΪ30�ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com