
【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线y=![]() x2+3x+1的一部分,如图所示.
x2+3x+1的一部分,如图所示.
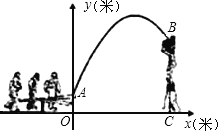
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
科目:初中数学 来源: 题型:
【题目】已知点M 到x 轴的距离为 7,到y 轴的距离为 2,则点M 的坐标为( )
A. (7,2) B. (-7,-2)
C. (7,-2) D. (2,7)或(2,-7)或(-2,7)或(-2,-7)
查看答案和解析>>
科目:初中数学 来源: 题型:
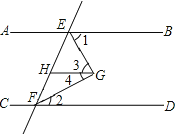
【题目】已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD
求证:∠EGF=90°
(1)把下列证明过程及理由补充完整.
(2 )请你用精炼准确的文字将上述结论总结出来.
证明:∵HG∥AB(已知)
∴∠1=∠3 ( )
又∵HG∥CD(已知)
∴∠2=∠4(同理)
∵AB∥CD(已知)
∴∠BEF+ =180° ( )
又∵EG平分∠BEF(已知)
∴∠1=![]() ∠
∠
又∵FG平分∠EFD(已知)
∴∠2=![]() ∠EFD (同理)
∠EFD (同理)
∴∠1+∠2=![]() ( + )
( + )
∴∠1+∠2=90°
∴∠3+∠4=90°
即∠EGF=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE. 将△EDC绕点C按顺时针方向旋转,记旋转角为α.
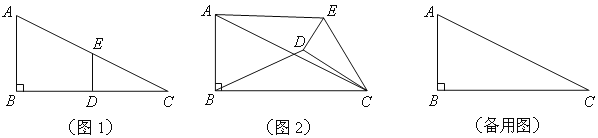
(1)问题发现
① 当![]() 时,
时,![]() ;
;
② 当![]() 时,
时,![]()
(2)拓展探究
试判断:当0°<α<360°时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△EDC旋转至A、D、E三点共线时,直接写出线段BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com