
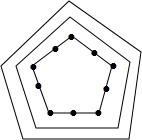
 在一次大型演出中,由1200名演员排出如图所示的正五边形队,内圈每边3人,往外每圈每边增加2人(即由内向外算起,第2圈每边5人,第三圈每边7人…),这样1200人恰好排完,则这个队共排了15圈.
在一次大型演出中,由1200名演员排出如图所示的正五边形队,内圈每边3人,往外每圈每边增加2人(即由内向外算起,第2圈每边5人,第三圈每边7人…),这样1200人恰好排完,则这个队共排了15圈. 分析 由题意可知:从内向外,第一圈共站(3-1)×5=10人,第二圈共站(5-1)×5=20人,第三圈共站(7-1)×5=30人,…由此得出第n圈共站(2n+1-1)×5=10n人,由此求和建立方程求得答案即可.
解答 解:∵从内向外,第一圈共站(3-1)×5=10人,
第二圈共站(5-1)×5=20人,
第三圈共站(7-1)×5=30人,
…
第n圈共站(2n+1-1)×5=10n人,
∴10+20+30+…+10n=1200
即10×$\frac{1}{2}$n(n+1)=1200
解得n=15
答:这个队共排了15圈.
故答案为:15.
点评 此题考查书图形的变化规律,找出图形之间的联系,得出运算规律,利用规律解决问题.


科目:初中数学 来源: 题型:解答题
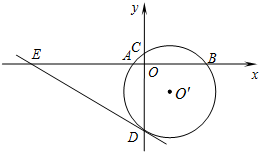 如图,已知⊙O′与x轴交于A、B两点,与y轴交于C、D两点,圆心O′的坐标是(1,-1),半径为$\sqrt{5}$.
如图,已知⊙O′与x轴交于A、B两点,与y轴交于C、D两点,圆心O′的坐标是(1,-1),半径为$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 划分次数 | 扇形总个数 |
| 1 | 6 |
| 2 | 11 |
| 3 | 16 |
| 4 | 21 |
| … | … |
| n | 5n+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在一个腰长为10的等腰直角三角形的内部作一个矩形ABCD,其中B,D分别在边AF,AE上,则此矩形的最大面积为( )
如图,在一个腰长为10的等腰直角三角形的内部作一个矩形ABCD,其中B,D分别在边AF,AE上,则此矩形的最大面积为( )| A. | 25 | B. | 24 | C. | 20 | D. | 18 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com