
����Ŀ����ͼ1����һ��ֱ�����ǰ����ͬһ��ֱ��AB�ϣ�����![]() ��
��![]() ��
��
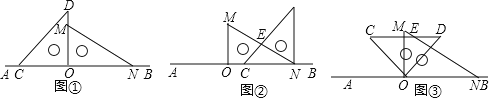
![]() ��ͼ1�е����dz�OCD��AB�ķ���ƽ����ͼ
��ͼ1�е����dz�OCD��AB�ķ���ƽ����ͼ![]() ��λ�ã�ʹ�õ�O���N�غϣ�CD��MN�ཻ�ڵ�E����
��λ�ã�ʹ�õ�O���N�غϣ�CD��MN�ཻ�ڵ�E����![]() �Ķ�����
�Ķ�����
![]() ��ͼ1�е����dz�OCD�Ƶ�O��˳ʱ�뷽����ת��ʹһ��OD��
��ͼ1�е����dz�OCD�Ƶ�O��˳ʱ�뷽����ת��ʹһ��OD��![]() ���ڲ�����ͼ3����ODǡ��ƽ��
���ڲ�����ͼ3����ODǡ��ƽ��![]() ��CD��MN�ཻ�ڵ�E����
��CD��MN�ཻ�ڵ�E����![]() �Ķ�����
�Ķ�����
![]() ��ͼ1�е����dz�OCD�Ƶ�O��ÿ��
��ͼ1�е����dz�OCD�Ƶ�O��ÿ��![]() ���ٶ���˳ʱ�뷽����תһ�ܣ�����ת�Ĺ����У��ڵ�______ ��ʱ����CDǡ�����MNƽ�У��ڵ�______ ��ʱ��ֱ��CDǡ����ֱ��MN��ֱ
���ٶ���˳ʱ�뷽����תһ�ܣ�����ת�Ĺ����У��ڵ�______ ��ʱ����CDǡ�����MNƽ�У��ڵ�______ ��ʱ��ֱ��CDǡ����ֱ��MN��ֱ![]() ֱ��д�����
ֱ��д�����![]()
���𰸡�(1)105��;(2)������;(3) 5��17��11��23��
����������1�����������ε��ڽǺͶ����ɵá�CEN=180�㩁��DCN����MNO���������ݼ��㼴�ɵý���
��2�����ݽ�ƽ���ߵĶ��������DON=45�㣬�����ڴ��������ֱ��ƽ�����CD��AB���ٸ�����ֱ��ƽ����ͬ���ڽǻ�����⼴����
��3���ٷ�CD��AB�Ϸ�ʱ��CD��MN����OM��CD�ཻ��F��������ֱ��ƽ����ͬλ����ȿɵá�OFD=��M=60�㣬Ȼ����������ε��ڽǺͶ�����ʽ�����MOD�����ɵý���CD��AB���·�ʱ��CD��MN����ֱ��OM��CD�ཻ��F��������ֱ��ƽ�����ڴ�����ȿɵá�DFO=��M=60�㣬Ȼ�����������ε��ڽǺͶ��������DOF���������ת�Ǽ������ڷ�CD��OM���ұ�ʱ����CD��AB�ཻ��G������ֱ������������ǻ��������CGN���ٸ��������ε�һ����ǵ������������ڵ������ڽǵĺ������CON���������ת�Ǽ�����CD��OM�����ʱ����CD��AB�ཻ��G������ֱ������������ǻ��������NGD���ٸ��������ε�һ����ǵ������������ڵ������ڽǵĺ���ʽ�����AOC��Ȼ�������ת�������㼴�ɵý⣮
��1���ڡ�CEN������CEN=180�㩁��DCN����MNO
=180�㩁45�㩁30��
=105�㣻
��2����ODƽ�֡�MON�����DON=![]() ��MPN=
��MPN=![]() ��90��=45�㣬���DON=��D=45�㣬��CD��AB�����CEN=180�㩁��MNO=180�㩁30��=150�㣻
��90��=45�㣬���DON=��D=45�㣬��CD��AB�����CEN=180�㩁��MNO=180�㩁30��=150�㣻
��3����ͼ1��CD��AB�Ϸ�ʱ����OM��CD�ཻ��F��
��CD��MN�����OFD=��M=60��������ODF������MOD=180�㩁��D����OFD=180�㩁45�㩁60��=75�㣬����ת��Ϊ75�㣬t=75����15��=5����
CD��AB���·�ʱ����ֱ��OM��CD�ཻ��F��
��CD��MN�����DFO=��M=60��������DOF������DOF=180�㩁��D����DFO=180�㩁45�㩁60��=75�㣬����ת��Ϊ75��+180��=255�㣬t=255����15��=17����
������������5��17��ʱ����CDǡ�����MNƽ����
��ͼ2��CD��OM���ұ�ʱ����CD��AB�ཻ��G��
��CD��MN�����NGC=90�㩁��MNO=90�㩁30��=60�㣬���CON=��NGC����OCD=60�㩁45��=15�㣬����ת��Ϊ180�㩁��CON=180�㩁15��=165�㣬t=165����15��=11����CD��OM�����ʱ����CD��AB�ཻ��G��
��CD��MN�����NGD=90�㩁��MNO=90�㩁30��=60�㣬���AOC=��NGD����C
������������11��23��ʱ��ֱ��CDǡ����ֱ��MN��ֱ��
�ʴ�Ϊ��5��17��11��23��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˷ḻѧ������С��������ѧ�����ֲ�������������ʦ��ѧ����5m���IJ����س�2m��1m�IJ������������ֹ���֯���ڲ�����˷ѵ�ǰ���£����м��ֲ�ͬ�Ľط���������
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
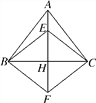
����Ŀ����ͼ���ڵ���������ABC�У�AB=AC��AH��BC����E��AH��һ�㣬�ӳ�AH����F��ʹFH=EH.
(1)��֤���ı���EBFC�����Σ�
(2)�����BAC=��ECF����֤��AC��CF.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ѧ������ѧ���п�չ��ɳ�����������������������������Ŀ�Ļ��Ϊ�˽�ѧ����������Ŀ��ϲ���������������˸�Уm��ѧ����ϲ����һ����Ŀ��ÿ��ѧ����ѡ��ֻ��ѡ�����ֻ��Ŀ��һ�֣����������������Ƴ����µIJ�������ͳ��ͼ����
ѧ����ϲ���Ļ��Ŀ������ͳ�Ʊ�
��Ŀ | ѧ���������� | �ٷֱ� |
��ɳ�� | 20 | 10% |
������ | 60 | p% |
������ | n | 40% |
����� | 40 | 20% |
����ͼ�����ṩ����Ϣ������������⣺
��1��m= ��n= ��p= ��
��2�������������Ϣֱ�Ӳ�ȫ����ͳ��ͼ��

��3�����ݳ�����������������Ƹ�У2000��ѧ�����ж�����ѧ����ϲ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��k��0����ͼ���뷴��������y= ![]() ��m��0����ͼ����A��B���㣬��x�ύ��C�㣬��A������Ϊ��n��6������C������Ϊ����2��0������tan��ACO=2��
��m��0����ͼ����A��B���㣬��x�ύ��C�㣬��A������Ϊ��n��6������C������Ϊ����2��0������tan��ACO=2�� 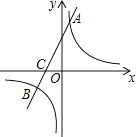
��1����÷�����������һ�κ����Ľ���ʽ��
��2�����B�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
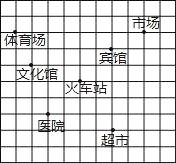
����Ŀ����ͼ������ij�в��ּ�ͼ��Ϊ��ȷ�����������λ�ã�
��1�������Ի�վΪԭ�㽨��ƽ��ֱ������ϵ��
��2��д���г�������Ϊ�� �������е�����Ϊ�� ����
��3���뽫������ΪA������ΪC�ͻ�վΪB�����������߶�������������ABC��Ȼ������������ƽ��4����λ���ȣ�����ƽ�ƺ����A1B1C1��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���B=90�㣬��E��AC���е㣬AC=2AB����BAC��ƽ����AD��BC�ڵ�D����AF��BC������DE���ӳ���AF�ڵ�F������FC��
��֤���ı���ADCF�����Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ABCD�У�AB��CD����ADC=90�㣬AB=AC������B��BE��AC�ڵ�E�� 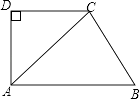
��1����֤����ADC�ա�BEA��
��2����AD=4��CD=3����BC�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com