
 在平面直角坐标系xOy中,二次函数y=2x2+bx+c的图象经过(-1,0)和($\frac{3}{2}$,0)两点.
在平面直角坐标系xOy中,二次函数y=2x2+bx+c的图象经过(-1,0)和($\frac{3}{2}$,0)两点.分析 (1)由二次函数的图象经过(-1,0)和($\frac{3}{2}$,0)两点,组成方程组再解即可求得二次函数的表达式;
(2)根据图象即可得出当-$\frac{3}{2}$<x<1时,y的取值范围;
(3)将一次函数 y=(1-k)x+2的图象向下平移k个单位后的一次函数表达式为y=(1-k)x+2-k,由题意得2x2-x-3=(1-k)x+2-k,整理得2x2+(k-2)x+k-5=0,因为m<2<n,m≠n,△=(k-2)2-4×2×(k-5)=(k-6)2+8>0,把x=2代入(1-k)x+2-k>2x2-x-3,解得k<$\frac{1}{3}$,所以m的取值范围为m<$\frac{1}{3}$的全体实数.
解答  解:(1)由二次函数的图象经过(-1,0)和($\frac{3}{2}$,0)两点.
解:(1)由二次函数的图象经过(-1,0)和($\frac{3}{2}$,0)两点.
∴$\left\{\begin{array}{l}{0=2-b+c}\\{0=\frac{9}{2}+\frac{3}{2}b+c}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=-1}\\{c=-3}\end{array}\right.$,
∴此二次函数的表达式y=2x2-x-3;
(2)当x=-$\frac{3}{2}$时,y=3,当x=1时,y=-2,
又∵二次函数的顶点坐标是($\frac{1}{4}$,-$\frac{25}{8}$)
∴当-$\frac{3}{2}$<x<1时,y的取值范围是-$\frac{25}{8}$≤y<3;
(3)将一次函数 y=(1-k)x+2的图象向下平移k个单位后的一次函数表达式为y=(1-k)x+2-k,
∵y=(1-k)x+2-k与二次函数y=2x2+bx+c图象交点的横坐标为m和n,
∴2x2-x-3=(1-k)x+2-k,整理得
2x2+(k-2)x+k-5=0
∵m<2<n
∴m≠n
∴△=(k-2)2-4×2×(k-5)=(k-6)2+8>0
∴k≠1
∵m<2<n
当x=2时,(1-k)x+2-k>2x2-x-3
把x=2代入(1-k)x+2-k>2x2-x-3,解得k<$\frac{1}{3}$
∴k的取值范围为k<$\frac{1}{3}$的全体实数.
点评 本题主要考查了求二次函数的解析式以及二次函数的图象与几何变换.


科目:初中数学 来源: 题型:选择题
| A. | ($\sqrt{6}$)2=±6 | B. | ($\sqrt{-7}$)2=-7 | C. | $\sqrt{3}$×$\sqrt{6}$=3$\sqrt{2}$ | D. | $\sqrt{6}$÷$\sqrt{3}$=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4.5×1011 | B. | 4.5×103 | C. | 4.5×1012 | D. | 45×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
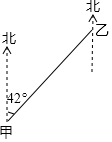 如图,在甲、乙两地之间修一条笔直的公路,从甲地测得公路的走向是北偏东42°,甲、乙两地同时开工,若干天后公路准确接通,乙地所修公路的走向是南偏西多少度?为什么?
如图,在甲、乙两地之间修一条笔直的公路,从甲地测得公路的走向是北偏东42°,甲、乙两地同时开工,若干天后公路准确接通,乙地所修公路的走向是南偏西多少度?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7.95×1012元 | B. | 79.5×1011元 | C. | 7.95×1011元 | D. | 7.95×1013元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com