练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．在x轴上求满足条件的点P，使它到点A（2，3）的距离等于5．

    分析 可设点P的坐标为（x，0），根据勾股定理得到关于AP的长的方程，解方程即可求解．

    解答 解：设点P的坐标为（x，0），则
    $\sqrt{（x-2）^{2}+{3}^{2}}$=5，
    解得x1=-2，x2=6．
    故点P的坐标为（-2，0）或（6，0）．

    点评 本题考查了点的坐标，坐标与图形性质，勾股定理的应用，得到AP的长的方程是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

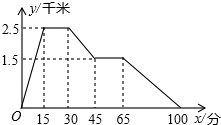    5．如图所示，图象反映的是：张阳从家里跑步去体育场，在那里锻炼了一阵后又走到文具店去买笔，然后走回家，其中x表示时间，y表示张阳离家的距离．根据图象回答下列问题：
    （1）体育场离张阳家2.5千米；
    （2）体育场离文具店1千米；张阳在文具店逗留了20分钟；
    （3）请计算：张阳从文具店到家的平均速度为每小时多少千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．如图所示，如果点A的位置为（3，2），那么点B的位置为（2，5），点C的位置为（4，4）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．我县某超市为提高销售量，在“国庆节”和“双十一”时让利于民，先后对某一款售价为625元/台的家用电器进行了两次相同幅度的降价．现在的实际销售价为400元/台．春节将至，该超市决定再一次让利于民，按前两次相同的幅度进行降价，请问过“春节”时该电器的售价是多少元/台？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．（1）如图1，AC=AE，∠1=∠2，AB=AD，求证：BC=DE；
    （2）如图2，∠ABC=38°，∠ACB=100°，AD平分∠BAC，AE是BC边上的高，求∠DAE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

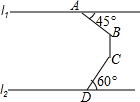    20．如图，在同一平面内，两条平行景观长廊l1和l2间有一条“U”形通道，其中AB段与景观长廊l1成45°角，长为20m；BC段与景观长廊垂直，长为10m，CD段与景观长廊l2成60°角，长为10m，求两景观长廊间的距离（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

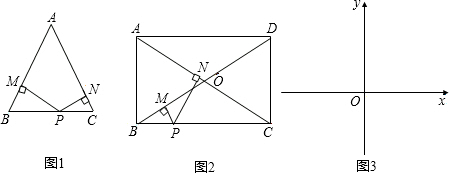
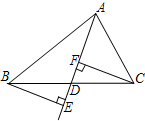    7．如图，已知BE⊥AD，CF⊥AD，BE=CF，由这三个条件组合运用可以得到若干结论，请你写出三个正确结论：△BDE≌△CDF，BD=CD，AD是△ABC的中线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．（1）如图1，等腰△ABC中，AB=AC，P是BC上任意一点，PM⊥AB于点M，PN⊥AC于点N．求证：PM+PN等于△ABC的腰上的高．
    （2）如图2，矩形ABCD中，AB=3cm，BC=4cm，P为BC边上任一点，PM⊥BD于点M，PN⊥AC于点N，且PM=1cm，求PN的长．
    （3）已知：直线l1：y=$\frac{\sqrt{3}}{3}$x+2，l2：y=-（$\sqrt{3}$+2）x+2，若l2上一点A到l1的距离为AB=1，求点A的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

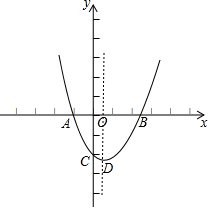    5．在平面直角坐标系中（如图），已知抛物线y=x2+bx+c与x轴交于点A（-1，0）和点B，与y轴交于点C（0，-2）．
    （1）求该抛物线的表达式，并写出其对称轴；
    （2）点D为该抛物线的顶点，设点P（t，0），且t＞3，如果△BDP和△CDP的面积相等，求t的值．

    查看答案和解析>>

    同步练习册答案