
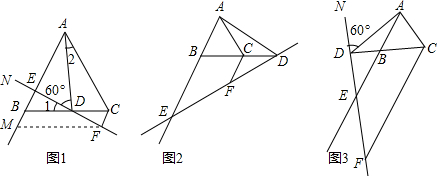
分析 (1)①根据等边三角形的性质∠ABC=∠ACB=60°,根据已知条件得到∠1+∠ADC=120°,∠ADC+∠2=120°,根据等式的性质即可得到结论;②通过△MEF≌△CDA即可求得ME=CD,因为通过证四边形BCFM是平行四边形可以得出BM=CF,从而证得CF+BE=CD;
(2)作FM∥BC,得出四边形BCFM是平行四边形,然后通过证得△MEF≌△CDA即可求得,
(3)根据△ABC的面积可求得AB=BC=AC=4,同时代的BD=2AB=8,求得 BE=8,即可得到结论.
解答 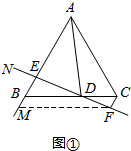 解:(1)①∠1=∠2,
解:(1)①∠1=∠2,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°
∵∠ADN=60°,
∴∠1+∠ADC=120°,∠ADC+∠2=120°,
∴∠1=∠2;
②证明:如图①,过点F作FM∥BC交射线AB于点M,
∵CF∥AB,
∴四边形BMFC是平行四边形,
∴BC=MF,CF=BM,
∴∠ABC=∠EMF,∠BDE=∠MFE,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,BC=AC,
∴∠EMF=∠ACB,AC=MF,
∵∠ADN=60°,
∴∠BDE+∠ADC=120°,∠ADC+∠DAC=120°,
∴∠BDE=∠DAC,
∴∠MFE=∠DAC,
在△MEF与△CDA中,
$\left\{\begin{array}{l}{∠MFE=∠DAC}\\{∠EMF=∠ACB}\\{MF=AC}\end{array}\right.$,
∴△MEF≌△CDA(AAS),
∴CD=ME=EB+BM,
∴CD=BE+CF;
(2)如图②,由(1)证得四边形BMFC是平行四边形,
∴BC=MF,CF=BM,
由(1)证得△MEF≌△CDA(AAS),
∴CD=ME=EB-BM,
∴CF+CD=BE,
如图③,同理CF-CD=BE;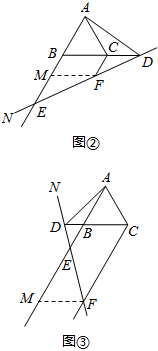
(3)∵△ABC是等边三角形,S△ABC=4$\sqrt{3}$,
∴易得AB=BC=AC=4,
如图②,
∵∠ADC=30°,∠ACB=60°,
∴CD=AC=4,
∵∠ADN=60°,
∴∠CDF=30°,
又∵CF∥AB,
∴∠BCF=∠ABC=60°,
∴∠CFD=∠CDF=30°,
∴CD=CF,
由(2)知BE=CF+CD,
∴BE=4+4=8.
如图③,
∵∠ADC=30°,∠ABC=60°,
∴∠BAD=∠ADC=30°,
∴BD=BA=4,
∴CD=BD+BC=4+4=8,
∵∠ADN=60°,∠ADC=30°,
∴∠BDE=90°,
又∵∠DBE=∠ABC=60°,
∴∠DEB=30°,
在Rt△BDE中,∠DEB=30°,BD=4,
∴BE=2BD=8,
综上,BE=8,CD=4或8.
点评 本题考查了等边三角形的性质,平行四边形的判定和性质,三角形全等的判定和性质,30°角所对的直角边等于斜边的一半,正确的作出辅助线构造全等三角形是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
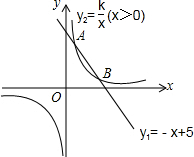 如图,一次函数y1=-x+5的图象与反比例函数y2=$\frac{k}{x}$(x>0)的图象相交于点A(m,4)和点B(4,n).
如图,一次函数y1=-x+5的图象与反比例函数y2=$\frac{k}{x}$(x>0)的图象相交于点A(m,4)和点B(4,n).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
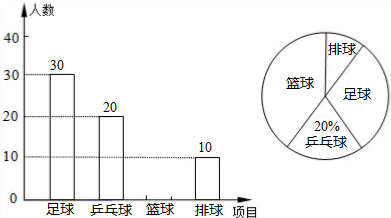
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
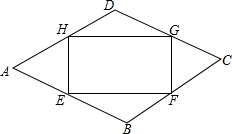 如图,某校园内有一块菱形的空地ABCD,为了美化环境,现要进行绿化,计划在中间建设一个面积为S的矩形绿地EFGH.其中,点E、F、G、H分别在菱形的四条边上,AB=a米,BE=BF=DG=DH=x米,∠A=60°
如图,某校园内有一块菱形的空地ABCD,为了美化环境,现要进行绿化,计划在中间建设一个面积为S的矩形绿地EFGH.其中,点E、F、G、H分别在菱形的四条边上,AB=a米,BE=BF=DG=DH=x米,∠A=60°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
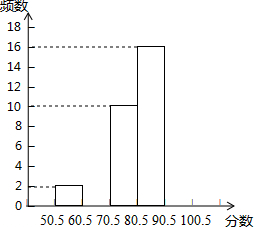 某校对600名学生进行了一次“心理健康”知识测试,从中抽取了部分学生成绩(得分取正整数,满分为100分)作为样本,绘制了下面尚未完成的表格和频数分布直方图(住:无50.5以下成绩)
某校对600名学生进行了一次“心理健康”知识测试,从中抽取了部分学生成绩(得分取正整数,满分为100分)作为样本,绘制了下面尚未完成的表格和频数分布直方图(住:无50.5以下成绩)| 分组 | 频数 | 频率 |
| 50.5~60.5 | 2 | 0.04 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | 10 | C |
| A~90.5 | B | 0.32 |
| 90.5~100.5 | 14 | 0.28 |
| 合计 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com