
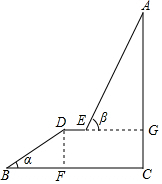
 如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车达到A处,返程时从A处乘坐升降电梯直接到达C处;已知:AC⊥BC于C,DE∥BC,BC=110米,DE=10米,BD=60米,BD=60米,α=30°,β=60°,求AC的高度.
如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车达到A处,返程时从A处乘坐升降电梯直接到达C处;已知:AC⊥BC于C,DE∥BC,BC=110米,DE=10米,BD=60米,BD=60米,α=30°,β=60°,求AC的高度. 分析 根据已知和余弦的概念求出DF的长,得到CG的长,根据正切的概念求出AG的长,求和得到答案.
解答 解:∵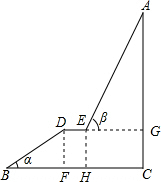 cos∠DBF=$\frac{BF}{BD}$,
cos∠DBF=$\frac{BF}{BD}$,
∴BF=60×$\frac{\sqrt{3}}{2}$=30$\sqrt{3}$(m),
FH=DE=10m,
∴EG=HC=110-30$\sqrt{3}$-10=(100-30$\sqrt{3}$)m,
∵tan∠AEG=$\frac{AG}{EG}$,
∴AG=(100-30$\sqrt{3}$)×$\sqrt{3}$=(100$\sqrt{3}$-90)m,
∵sin∠DBF=$\frac{DF}{BD}$,
∴DF=60×$\frac{1}{2}$=30(m),
∴CG=30m,
∴AC=AG+CG=100$\sqrt{3}$-90+30=(100$\sqrt{3}$-60)米,
答:AC的高度为(100$\sqrt{3}$-60)米.
点评 本题考查的是解直角三角形的应用,掌握锐角三角函数的概念和坡角的概念是解题的关键,解答时注意:正确作出辅助线构造直角三角形准确运用锐角三角函数的概念列出算式.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在同一平面内,过一点可作一条直线与已知直线垂直 | |
| B. | 过一点可作一条直线与已知直线平行 | |
| C. | 三条直线两两相交有三个交点 | |
| D. | 垂直于同一条直线的两条直线平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
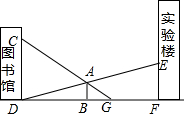 某中学的图书馆与实验楼中间有一地标牌AB,小鸣和小夕两位同学分别在图书馆和实验楼的C、E两点处观测地标牌的顶端A,他们的视线如图所示,小鸣从点C处可以看到地面上距离实验楼底部10米远的点G处,小夕从点E恰好可以看到图书馆的底部D处,已知图中的所有点均在同一平面内,CD⊥DF,AB⊥DF,EF⊥DF,CD=6米,EF=3米,DF=25米,请你根据以上数据,求该地标牌的高度AB及它与图书馆之间的距离BD(结果精确到0.1米).
某中学的图书馆与实验楼中间有一地标牌AB,小鸣和小夕两位同学分别在图书馆和实验楼的C、E两点处观测地标牌的顶端A,他们的视线如图所示,小鸣从点C处可以看到地面上距离实验楼底部10米远的点G处,小夕从点E恰好可以看到图书馆的底部D处,已知图中的所有点均在同一平面内,CD⊥DF,AB⊥DF,EF⊥DF,CD=6米,EF=3米,DF=25米,请你根据以上数据,求该地标牌的高度AB及它与图书馆之间的距离BD(结果精确到0.1米).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
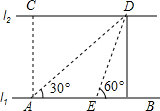 如图,河的两岸l1与l2互相平行,A、B是l1上的两点,C、D是l2上的两点,某同学在A处测得∠CAB=90°,∠DAB=30°,再沿AB方向走20米到达点E(即AE=20),测得∠DEB=60°.
如图,河的两岸l1与l2互相平行,A、B是l1上的两点,C、D是l2上的两点,某同学在A处测得∠CAB=90°,∠DAB=30°,再沿AB方向走20米到达点E(即AE=20),测得∠DEB=60°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
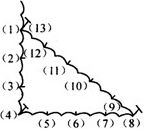 古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( )
古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( )| A. | 直角三角形两个锐角互补 | |
| B. | 三角形内角和等于180° | |
| C. | 如果三角形两条边长的平方和等于第三边长的平方 | |
| D. | 如果三角形两条边长的平方和等于第三边长的平方,那么这个三角形是直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知?OABC,在平面直角坐标系中,A(5,0),C(1,3),直线y=kx-2与BC、OA分别交于M,N,且将?OABC的面积分成相等的两部分,则k的值是k=$\frac{7}{6}$.
如图,已知?OABC,在平面直角坐标系中,A(5,0),C(1,3),直线y=kx-2与BC、OA分别交于M,N,且将?OABC的面积分成相等的两部分,则k的值是k=$\frac{7}{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com