
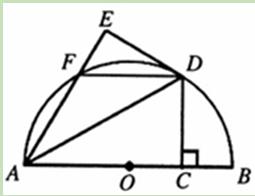
(11·十堰)如图,AB是半圆O的直径,点C为半径OB上一点,过点C作CD⊥AB交半圆O于点D,将△ACD沿AD折叠 得到△AED,AE交半圆于点F,连接DF。
得到△AED,AE交半圆于点F,连接DF。
(1)求证:DE是半圆的切线;
(2)连接OD,当OC=BC时,判断四边形ODFA的形状,并证明你的结论。
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
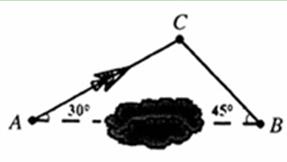
科目:初中数学 来源:2011年初中毕业升学考试(山东济南卷)数学解析版 题型:解答题
(11·十堰)如图,一架飞机从A地飞往B地,两地相距600km.飞行员为了避开某一区域的雷雨去层,从机场起飞以后,就沿与原来的飞行方向成300 角的方向飞行,飞行到中途,再沿与原来的飞行方向成450角的方向继续飞行直到终
角的方向飞行,飞行到中途,再沿与原来的飞行方向成450角的方向继续飞行直到终 点。这样飞机的飞行路程比原来的路程控交换机600km远了多少?
点。这样飞机的飞行路程比原来的路程控交换机600km远了多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com