

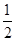 ∠AOC,计算即可得解;
∠AOC,计算即可得解;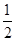 ∠AOC=
∠AOC=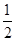 ×80°=40°;
×80°=40°;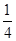 ∠AOC=
∠AOC=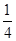 ×80°=20°,
×80°=20°,

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,∠EAC+∠FBC=
,∠EAC+∠FBC=
 与
与 有何关系?并说明理由.
有何关系?并说明理由.
 、
、 的关系是 .(用
的关系是 .(用 、
、 表示)
表示)
 ≥
≥ ,∠EAC与∠FBC的平分线相交于
,∠EAC与∠FBC的平分线相交于 ,
,  ;依此类推,则
;依此类推,则 = (用
= (用 、
、 表示)
表示)
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com