
【题目】已知∠AOB=120°,OC、OD过点O的射线,射线OM、ON分别平分∠AOC和∠DOB.
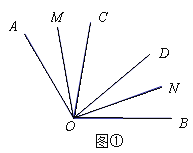
(1)如图①,若OC、OD是∠AOB 的三等分线,求∠MON的度数;
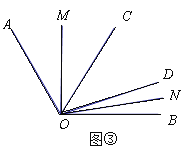
(2)如图②,若∠COD=50°,∠AOC≠∠DOB,则∠MON= °;
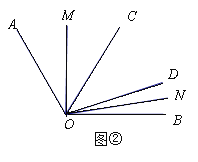
(3)如图③,在∠AOB内,若∠COD=α(0°<α<60°),则∠MON= °.
【答案】(1)∠MON =80°;(2)85°;(3)![]()
【解析】试题分析:(1)根据角平分线的定义得到∠AOC=∠COD=∠DOB=![]() ×120°=40°,∠MOC=∠AOC=20°,∠DON=∠DOB=20°,则∠MON=20°+40°+20°=80°;
×120°=40°,∠MOC=∠AOC=20°,∠DON=∠DOB=20°,则∠MON=20°+40°+20°=80°;
(2)根据角平分线的定义得到∠MOC=![]() ∠AOC,∠DON=
∠AOC,∠DON=![]() ∠DOB,而∠AOC+∠DOB=120°-50°=70°,则∠MOC+∠DON=35°,所以∠MON=50°+35°=85°;
∠DOB,而∠AOC+∠DOB=120°-50°=70°,则∠MOC+∠DON=35°,所以∠MON=50°+35°=85°;
(3)与(2)一样得到∠AOC+∠DOB=120°-α,∠MOC+∠DON=60°-![]() α,则∠MON=60°-
α,则∠MON=60°-![]() α+α=60°+
α+α=60°+![]() α.
α.
试题解析:(1)∵OC,OD是∠AOB的三等分线,
∴∠AOC=∠COD=∠DOB=![]() ∠AOB=
∠AOB=![]() ×120°=40°,
×120°=40°,
∵OM平分∠AOC,ON平分∠DOB,
∴∠MOC=![]() ∠AOC=20°, ∠DON=
∠AOC=20°, ∠DON=![]() ∠DOB=20° ,
∠DOB=20° ,
∴∠MON=∠MOC+∠COD+∠DON=80°;
(2)∵射线OM、ON分别平分∠ACO和∠DOB,
∴∠MOC=![]() ∠AOC,∠DON=
∠AOC,∠DON=![]() ∠DOB,
∠DOB,
∴∠MOC+∠DON=![]() (∠AOC+∠DOB),
(∠AOC+∠DOB),
∵∠AOB=120°,∠COD=50°,
∴∠AOC+∠DOB=120°-50°=70°,
∴∠MOC+∠DON=35°,
∴∠MON=50°+35°=85°,
故答案为:85;
(3)∵射线OM、ON分别平分∠AOC和∠DOB,
∴∠MOC=![]() ∠AOC,∠DON=
∠AOC,∠DON=![]() ∠DOB,
∠DOB,
∴∠MOC+∠DON=![]() (∠AOC+∠DOB),
(∠AOC+∠DOB),
∵∠AOB=120°,∠COD=α,
∴∠AOC+∠DOB=120°-α,
∴∠MOC+∠DON=60°-![]() α,
α,
∴∠MON=60°-![]() α+α=60°+
α+α=60°+![]() α=
α=![]() ,
,
故答案为: ![]() .
.


科目:初中数学 来源: 题型:
【题目】陈老师和学生做一个猜数游戏,他让学生按照如下步骤进行计算:
①任想一个两位数a,把a乘以2,再加上9,把所得的和再乘以2;
②把a乘以2,再加上30,把所得的和除以2;
③把①所得的结果减去②所得的结果,这个差即为最后的结果.
陈老师说:只要你告诉我最后的结果,我就能猜出你最初想的两位数a.
学生周晓晓计算的结果是96,陈老师立即猜出周晓晓最初想的两位数是31.
请完成
(1)由①可列代数式 ,由②可列代数式 ,由③可知最后结果为 ;(用含a的式子表示)
(2)学生小明计算的结果是120,你能猜出他最初想的两位数是多少吗?
(3)请用自己的语言解释陈老师猜数的方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点A,B,C在同一条直线上,点M、N分别是AB、AC的中点,如果AB=10cm,AC=8cm,那么线段MN的长度为( )
A. 6cm B. 9cm C. 3cm或6cm D. 1cm或9cm
查看答案和解析>>
科目:初中数学 来源: 题型:
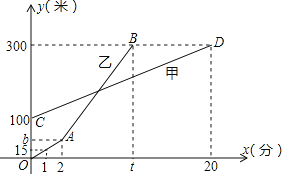
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米.
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题的过程中,我们常用到 “分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答问题.
【提出问题】三个有理数![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
【解决问题】
解:由题意,得![]() 三个有理数都为正数或其中一个为正数,另两个为负数.
三个有理数都为正数或其中一个为正数,另两个为负数.
①![]() 都是正数,即
都是正数,即![]() 时,则
时,则![]() ;
;
②当![]() 中有一个为正数,另两个为负数时,不妨设
中有一个为正数,另两个为负数时,不妨设![]() ,则
,则![]() .
.
综上所述, ![]() 值为3或-1.
值为3或-1.
【探究】请根据上面的解题思路解答下面的问题:
(1)三个有理数![]() 满足
满足![]() ,求
,求![]() 的值;
的值;
(2)若![]() 为三个不为0的有理数,且
为三个不为0的有理数,且![]() ,求
,求![]() 的值
的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com