
(本题14分)在平面直角坐标系中,已知抛物线经过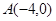 、
、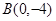 、
、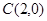 三点.
三点.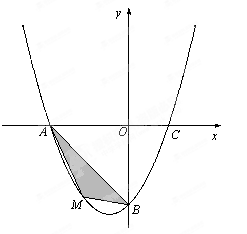
⑴ 求抛物线的解析式;
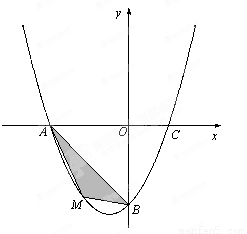
⑵ 若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值;
⑶ 若点P是抛物线上的动点,点Q是直线 上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
(1)抛物线的解析式为 y=x²/2+x-4
(2)作MN垂直x轴于N,则
S△AMB=S梯形OBMN+S△NMA-S△ABO
=1/2|-4-(m²/2+m-4)||m|+1/2|m²/2+m-4||-4-m|-8
=-m²-4m (-4<m<0)
即S关于M的函数关系式为 S(m)=-m²-4m (-4<m<0)
-m²-4m =-m(m+4)≤(-m+m+4)²/4=4,当m=-2时取等号,则
S(m)max=S(-2)=4
(3)要满足使点P,Q,B,O为顶点的四边形为平行四边形,可分为两种情况
第一种情况是OB为四边形的一边,要使其为平行四边形,则OB平行且等于PQ,即|x²/2+x-4+x|=4
x1=2√5-2,x2=-2√5-2,x3=-4
此时Q点坐标为(2√5-2,2-2√5)、(-2√5-2,2√5+2)或(-4,4)
第二种情况是OB为四边形的对角线,则OQ必为四边形的一边,要使其为平行四边形,则OQ平行且等于PB
过点B且平行于OQ的直线为 y=-x-4
与抛物线 y=x²/2+x-4 的另一交点为P(-4,0),|PB|=4√2
|OQ|=|PB|,则Q点为(4,-4)
综上所述,Q点坐标为(2√5-2,2-2√5)、(-2√5-2,2√5+2)、(-4,4)或(4,-4)时满足题意
解析


科目:初中数学 来源: 题型:
(本题14分)在平面直角坐标系中,已知抛物线经过![]() 、
、![]() 、
、![]() 三点.
三点.

⑴求抛物线的解析式;
⑵若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值;
⑶若点P是抛物线上的动点,点Q是直线![]() 上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
(本题14分)在同一平面直角坐标系中有6个点![]() ,
,![]() ,
,![]() .
.
(1)画出![]() 的外接圆⊙P,并指出点
的外接圆⊙P,并指出点![]() 与⊙P的位置关系;
与⊙P的位置关系;
(2)若将直线![]() 沿
沿![]() 轴向上平移,当它经过点
轴向上平移,当它经过点![]() 时,设此时的直线为
时,设此时的直线为![]() .
.
①判断直线![]() 与⊙P的位置关系,并说明理由;
与⊙P的位置关系,并说明理由;
②再将直线![]() 绕点
绕点![]() 按顺时针方向旋转,当它经过点
按顺时针方向旋转,当它经过点![]() 时,设此时的直线为
时,设此时的直线为![]() .求直线
.求直线![]() 与⊙P的劣弧
与⊙P的劣弧![]() 围成的图形的面积S(结果保留
围成的图形的面积S(结果保留![]() ).
).

查看答案和解析>>
科目:初中数学 来源:2011-2012年江苏省南通市幸福中学九年级上学期期中考试数学卷 题型:解答题
(本题14分)在同一平面直角坐标系中有6个点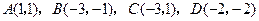 ,
, ,
, .
.
(1)画出 的外接圆⊙P,并指出点
的外接圆⊙P,并指出点 与⊙P的位置关系;
与⊙P的位置关系;
(2)若将直线 沿
沿 轴向上平移,当它经过点
轴向上平移,当它经过点 时,设此时的直线为
时,设此时的直线为 .
.
①判断直线 与⊙P的位置关系,并说明理由;
与⊙P的位置关系,并说明理由;
②再将直线 绕点
绕点 按顺时针方向旋转,当它经过点
按顺时针方向旋转,当它经过点 时,设此时的直线为
时,设此时的直线为 .求直线
.求直线 与⊙P的劣弧
与⊙P的劣弧 围成的图形的面积S(结果保留
围成的图形的面积S(结果保留 ).
).
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省泰州市九年级下学期质量检测数学卷 题型:解答题
(本题14分)在平面直角坐标系中,已知抛物线经过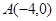 、
、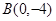 、
、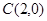 三点.
三点.
⑴ 求抛物线的解析式;
⑵ 若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值;
⑶
若点P是抛物线上的动点,点Q是直线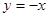 上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com