Question

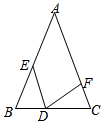
1．如图，在△ABC中，AB=AC，BD=CF，BE=CD，若∠A=40°，则∠EDF的度数为（　　）

• A． 75°
• B． 70°
• C． 65°
• D． 60°

Answer 1

分析 利用等腰三角形的性质及三角形内角和定理先求出∠B、∠C的度数，利用SAS判定△BED≌△CDF，从而得出对应角相等，再利用角与角之间的关系从而求得所求的角．

解答 解：∵AB=AC，∠A=40°
∴∠B=∠C=70°
∵EB=BD=DC=CF
∵△BED和△CDF中，
$\left\{\begin{array}{l}{BE=CD}\\{∠B=∠C}\\{BD=CF}\end{array}\right.$
∴△BED≌△CDF（SAS）
∴∠BDE=∠CFD，∠BED=∠CDF
∵∠EDF=180°-∠CDF-∠BDE=180°-（∠CDF+∠BDE）
∵∠B=70°
∴∠BDE+∠BED=110°即∠CDF+∠BDE=110°
∴∠EDF=180°-110°=70°．
故选B．

点评 本题考查了等腰三角形的性质及三角形内角和定理；注意发现三个等腰三角形，根据等腰三角形的两个底角相等以及三角形的内角和定理进行求解是解答本题的关键．