
【题目】如图,DE是AB的垂直平分线.
(1)已知AC=5cm,△ADC的周长为17cm,则BC的长__________
(2)若AD平分∠BAC,AD=AC,则∠C= __________

【答案】12cm 72°
【解析】
(1)要求BC的大小,只要求出CD+BD,由线段的垂直平分线的性质知BD=AD,结合三角形的周长可得答案;
(2)设∠BAD=x.由垂直平分线的性质得到AD=BD,由等边对等角得到∠B=∠BAD=x,由三角形外角的性质得到∠ADC=∠B+∠BAD= 2x.由等腰三角形的性质得到∠C=∠ADC=2x.由角平分线的性质得到∠CAD=∠BAD=x.在△ADC中,由三角形内角和定理列方程得到x的值,即可得到结论.
(1)∵DE是边AB的垂直平分线,∴AD=BD,∴△ADC的周长=AD+DC+AC=BD+DC+AC=BC+AC=17cm.
又∵AC=5cm,∴BC=12cm.
(2)设∠BAD=x.
∵DE是边AB的垂直平分线,∴AD=BD,∴∠B=∠BAD=x,∴∠ADC=∠B+∠BAD=x+x=2x.
∵AD=AC,∴∠C=∠ADC=2x.
∵AD平分∠BAC,∴∠CAD=∠BAD=x.在△ADC中,x+2x+2x=180°,解得:x=36°,∴∠C=2x=72°.
故答案为:12cm,72°.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】科技馆是少年儿童节假日游玩的乐园.如图所示,图中点的横坐标x表示科技馆从8:30开门后经过的时间(分钟),纵坐标y表示到达科技馆的总人数.图中曲线对应的函数解析式为y= ![]() ,10:00之后来的游客较少可忽略不计.
,10:00之后来的游客较少可忽略不计.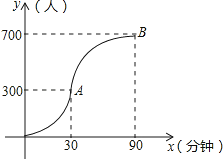
(1)请写出图中曲线对应的函数解析式;
(2)为保证科技馆内游客的游玩质量,馆内人数不超过684人,后来的人在馆外休息区等待.从10:30开始到12:00馆内陆续有人离馆,平均每分钟离馆4人,直到馆内人数减少到624人时,馆外等待的游客可全部进入.请问馆外游客最多等待多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的周长是16,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D且OD=2,△ABC的面积是________________.
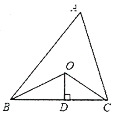
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
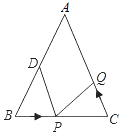
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是 ![]() 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2
的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2 ![]() 时,则阴影部分的面积为( )
时,则阴影部分的面积为( ) 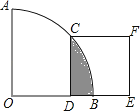
A.2π﹣4
B.4π﹣8
C.2π﹣8
D.4π﹣4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com