练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

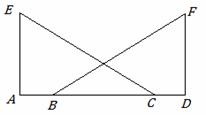
     已知：如图，点A、B、C、D在同一条直线上，EA⊥AD，FD⊥AD，AE=DF，AB=DC．

    求证：∠ACE=∠DBF．

                                         

                


     证明：∵AB=DC

    ∴AC=DB

    ∵EA⊥AD，FD⊥AD

    ∴∠A=∠D=90°

    在△EAC与△FDB中

    ∴△EAC≌△FDB

    ∴∠ACE=∠DBF．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    一个多边形的内角和是它的外角和的4倍，求这个多边形的边数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，若D为BC中点，那么用“SSS”判定△ABD≌△ACD需添加的一个条件是 ___________．

    第13题图
     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


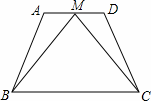
    如图，梯形ABCD中，AD∥BC，点M是AD的中点，且MB=MC，若AD=4，AB=6，BC=8，则梯形ABCD的周长为（　　）

    A．22 　　　  　B．24 　　　  　C．26 　　 　　D．28

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知△ABC，BA=BC，BD平分∠ABC，若∠C=40°，则∠ABE为         度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知∠1=∠2，则不一定能使△ABD≌△ACD的条件是（　　）

    A. AB=AC        B. BD=CD       C. ∠B=∠C      D.∠BDA=∠CDA

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知△ABC的六个元素，则下列甲、乙、丙三个三角形中和△ABC全等的图形是       

    第9题图
     
          

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如果两个直角三角形的两条直角边对应相等,那么两个直角三角形全等的

    依据是(   )

    ­  A. AAS­        B.SAS­        C.HL­         D.SSS

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    （1）班同学上数学活动课，利用角尺平分一个角（如图所示）．设计了如下方案：

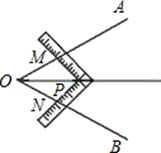
    （Ⅰ）∠AOB是一个任意角，将角尺的直角顶点P介于射线OA、OB之间，移动角尺使角尺两边相同的刻度与M、N重合，即PM=PN，过角尺顶点P的射线OP就是∠AOB的平分线．

    （Ⅱ）∠AOB是一个任意角，在边OA、OB上分别取OM=ON，将角尺的直角顶点P介于射线OA、OB之间，移动角尺使角尺两边相同的刻度与M、N重合，即PM=PN，过角尺顶点P的射线OP就是∠AOB的平分线．

    （1）方案（Ⅰ）、方案（Ⅱ）是否可行？若可行，请证明；若不可行，请说明理由；

    （2）在方案（Ⅰ）PM=PN的情况下，继续移动角尺，同时使PM⊥OA，PN⊥OB．此方案是否可行？请说明理由．

    查看答案和解析>>

    同步练习册答案