
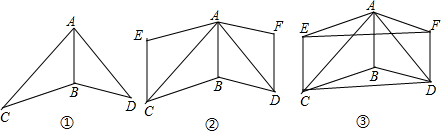
分析 (1)根旋转的性质得AB=DF,BD=FA,由于AB=BD,所以AB=BD=DF=FA,则可根据菱形的判定方法得到四边形ABDF是菱形;
(2)由于四边形ABDF是菱形,则AB∥DF,且AB=DF,再根据旋转的性质易得四边形ABCE为平行四边形,根据平行四边形的性质得AB∥CE,且AB=CE,所以CE∥FD,CE=FD,所以可判断四边形CDEF是平行四边形.
解答 (1)解:四边形ABDF是菱形.理由如下:
∵△ABD绕着边AD的中点旋转180°得到△DFA,
∴AB=DF,BD=FA,
∵AB=BD,
∴AB=BD=DF=FA,
∴四边形ABDF是菱形;
(2)证明:∵四边形ABDF是菱形,
∴AB∥DF,且AB=DF,
∵△ABC绕着边AC的中点旋转180°得到△CEA,
∴AB=CE,BC=EA,
∴四边形ABCE为平行四边形,
∴AB∥CE,且AB=CE,
∴CE∥FD,CE=FD,
∴四边形CDEF是平行四边形.
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了平行四边形的判定和菱形的判定.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:解答题
| 分值 | 16 | 15 | 14 | 13 | 12 | 10 | 8 | 6 | 3 | |
| 成绩 | 男(次) | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0.5 |
| 女(次) | 45 | 40 | 36 | 32 | 28 | 25 | 22 | 20 | <19 | |

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
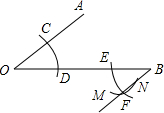 如图,用尺规作出了BF∥OA,作图痕迹中,弧MN是( )
如图,用尺规作出了BF∥OA,作图痕迹中,弧MN是( )| A. | 以B为圆心,OD长为半径的弧 | B. | 以C为圆心,CD长为半径的弧 | ||
| C. | 以E为圆心,DC长为半径的弧 | D. | 以E为圆心,OD长为半径的弧 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4200(1+x)2=6500 | B. | 4200(1+2x)=6500 | C. | 6500(1-x)2=4200 | D. | 6500(1-2x)=4200 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.
如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AB=AC,∠BAC=50?.分别以B、C为圆心,BC长为半径画弧,设两弧交于点D,与AB、AC的延长线分别交于点E、F,连接AD.则
如图,在△ABC中,AB=AC,∠BAC=50?.分别以B、C为圆心,BC长为半径画弧,设两弧交于点D,与AB、AC的延长线分别交于点E、F,连接AD.则查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | c<3 | B. | m≤$\frac{1}{2}$ | C. | n≤2 | D. | b<1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com