
【题目】操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰直角三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点.图1,2,3是旋转三角板得到的图形中的3种情况.
研究:
(1)三角板绕点P旋转,观察线段PD和PE之间有什么数量关系,并结合图2加以证明;
(2)三角板绕点P旋转,△PBE是否能成为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长);若不能,请说明理由;
(3)若将三角板的直角顶点放在斜边AB上的M处,且AM:MB=1:3,和前面一样操作,试问线段MD和ME之间有什么数量关系?并结合图4加以证明.
【答案】
(1)解:连接PC.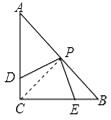
∵△ABC是等腰直角三角形,P是AB的中点,
∴CP=PB,CP⊥AB,∠ACP= ![]() ∠ACB=45°.
∠ACB=45°.
∴∠ACP=∠B=45°.
又∵∠DPC+∠CPE=∠BPE+∠CPE=90°,
∴∠DPC=∠BPE.
∴△PCD≌△PBE.
∴PD=PE
(2)解:共有四种情况:
①当点C与点E重合,即CE=0时,PE=PB;
②CE=2﹣ ![]() ,此时PB=BE;
,此时PB=BE;
③当CE=1时,此时PE=BE;
④当E在CB的延长线上,且CE=2+ ![]() 时,此时PB=EB
时,此时PB=EB
(3)解:MD:ME=1:3.
过点M作MF⊥AC,MH⊥BC,垂足分别是F、H.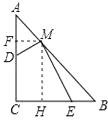
∴MH∥AC,MF∥BC.
∴四边形CFMH是平行四边形.
∵∠C=90°,
∴CFMH是矩形.
∴∠FMH=90°,MF=CH.
∵ ![]() ,HB=MH,
,HB=MH,
∴ ![]() .
.
∵∠DMF+∠DMH=∠DMH+∠EMH=90°,
∴∠DMF=∠EMH.
∵∠MFD=∠MHE=90°,
∴△MDF∽△MEH.
∴ ![]() .
.
【解析】本题等腰三角形的判定与性质.本题考查了等腰三角形的性质与判定;此题是分类讨论题,应分情况进行论证,不能漏解.辅助线的作出是解答本题的关键.
(1)连接PC,通过证明△DPC≌△EPB,得出PD=PE.
(2)分EP=EB、EP=PB时、BE=BP三种情况进行解答.
【考点精析】认真审题,首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°),还要掌握勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】在“家电下乡”活动期间,凡购买指定家用电器的农村居民均可得到该商品售价13%的财政补贴.村民小李购买了一台A型洗衣机,小王购买了一台B型洗衣机两人一共得到财政补贴351元,又知B型洗衣机售价比A型洗衣机售价多500元.求:
(1)A型洗衣机和B型洗衣机的售价各是多少元?
(2)小李和小王购买洗衣机除财政补贴外实际各付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人同时登西山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图11所示,乙在A处提速后的速度是甲登山速度的3.根据图象所提供的信息解答下列问题中正确的个数为( )

(1)甲登山的速度是每分钟10米.
(2)乙在A地提速时距地面的高度b为30米.
(3)登山9分钟时,乙追上了甲.
(4)乙在距地面的高度为165米时追上甲.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系内,正方形如图摆放,已知顶点 A(a,0),B(0,b) ,则顶点C的坐标为( )
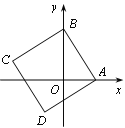
A.(-b,a b)B.(-b,b - a)C.(-a,b - a)D.(b,b -a)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算T,规定:T(x,y)=ax+2by﹣1(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=a0+2b1﹣1=2b﹣1.
(1)已知T(1,﹣1)=﹣2,T(4,2)=3.
①求a,b的值;
②若关于m的不等式组![]() 恰好有2个整数解,求实数p的取值范围;
恰好有2个整数解,求实数p的取值范围;
(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的实验时,绘出的某一结果出现的频率折线图,则符合这一结果的实验可能是( )

A. 抛一枚硬币,出现正面朝上
B. 掷一个正六面体的骰子,出现3点朝上
C. 一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D. 从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC的一角折叠,使点C落在△ABC内一点
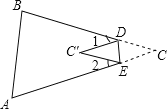
(1)若∠1=40°,∠2=30°,求∠C的度数;(2)试通过第(1)问,直接写出∠1、∠2、∠C三者之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,在斜边AB上分别截取AD=AC,BE=BC,DE=6,
点O是△CDE的外心,如图所示,则点O到△ABC的三边的距离之和是 . 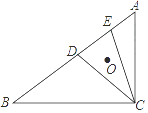
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C.
(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为2 ![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com