[题目]将1...按如图方式排列.若规定(m.n)表示第m排从左向右第n个数.则(6.5)与(13.6)表示的两数之积是( )A.B.6C.D. 题目和参考答案——青夏教育精英家教网—

【题目】将1、、、按如图方式排列，若规定（m、n）表示第m排从左向右第n个数，则（6，5）与（13，6）表示的两数之积是（）

A.B.6C.D.

【答案】B

【解析】

根据数的排列方法可知，第一排：1个数，第二排2个数．第三排3个数，第四排4个数，…第m-1排有（m-1）个数，从第一排到（m-1）排共有：1+2+3+4+…+（m-1）个数，根据数的排列方法，每四个数一个轮回，根据题目意思找出第m排第n个数到底是哪个数后再计算．

第一排1个数，第二排2个数．第三排3个数，第四排4个数，

…第m-1排有（m-1）个数，从第一排到（m-1）排共有：1+2+3+4+…+（m-1）个数，

根据数的排列方法，每四个数一个轮回，

由此可知：（6，5）表示第6排从左向右第5个数是，

（13，6）表示第13排从左向右第6个数，可以看出奇数排最中间的一个数都是1，

第13排是奇数排，最中间的也就是这排的第7个数是1，那么第6个就是，

则（6，5）与（13，6）表示的两数之积是6．

故选B．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】小聪在用描点法画二次函数y=ax2＋bx＋c的图象时，列出下面的表格：

x	…	－5	－4	－3	－2	－1	…
y	…	－7.5	－2.5	0.5	1.5	0.5	…

根据表格提供的信息，下列说法错误的是（）.

A. 该抛物线的对称轴是直线x=－2

B. b2－4ac＞0

C. 该抛物线与y轴的交点坐标为(0，－3.5)

D. 若(0.5，y1)是该抛物线上一点．则y1＜－2.5

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知函数y=|x2﹣x﹣2|，直线y=kx+4恰好与y=|x2﹣x﹣2|的图象只有三个交点，则k的值为_____．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在梯形中，，若，，，分别是梯形各边、、、的中点．

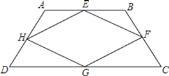
求证：四边形平行四边形；

当梯形满足什么条件时，四边形是菱形；

在的条件下，梯形满足什么条件时，四边形是正方形．

查看答案和解析>>

科目：初中数学 来源： 题型：

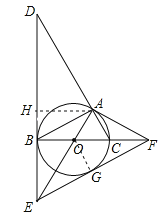
【题目】如图，⊙O是△ABC的外接圆，BC是⊙O的直径，∠ABC=30°，过点B作⊙O的切线BD，与CA的延长线交于点D，与半径AO的延长线交于点E，过点A作⊙O的切线AF，与直径BC的延长线交于点F．

（1）求证：△ACF∽△DAE；

（2）若S△AOC=，求DE的长；

（3）连接EF，求证：EF是⊙O的切线．

【答案】(1) 见解析; (2)3 ;(3)见解析.

【解析】试题分析：（1）根据圆周角定理得到∠BAC=90°，根据三角形的内角和得到∠ACB=60°根据切线的性质得到∠OAF=90°，∠DBC=90°，于是得到∠D=∠AFC=30°由相似三角形的判定定理即可得到结论；

（2）根据S△AOC=，得到S△ACF=，通过△ACF∽△DAE，求得S△DAE=，过A作AH⊥DE于H，解直角三角形得到AH=DH=DE，由三角形的面积公式列方程即可得到结论；

（3）根据全等三角形的性质得到OE=OF，根据等腰三角形的性质得到∠OFG=（180°﹣∠EOF）=30°，于是得到∠AFO=∠GFO，过O作OG⊥EF于G，根据全等三角形的性质得到OG=OA，即可得到结论．

试题解析：（1）证明：∵BC是⊙O的直径，∴∠BAC=90°，∵∠ABC=30°，∴∠ACB=60°

∵OA=OC，∴∠AOC=60°，∵AF是⊙O的切线，∴∠OAF=90°，∴∠AFC=30°，∵DE是⊙O的切线，∴∠DBC=90°，∴∠D=∠AFC=30，∵∠DAE=ACF=120°，∴△ACF∽△DAE；

（2）∵∠ACO=∠AFC+∠CAF=30°+∠CAF=60°，∴∠CAF=30°，∴∠CAF=∠AFC，∴AC=CF，∴OC=CF，∵S△AOC=，∴S△ACF=，∵∠ABC=∠AFC=30°，∴AB=AF，∵AB=BD，∴AF=BD，∴∠BAE=∠BEA=30°，∴AB=BE=AF，∴，∵△ACF∽△DAE，∴=，∴S△DAE=，过A作AH⊥DE于H，∴AH=DH=DE，∴S△ADE=DEAH=×=，∴DE=；

（3）∵∠EOF=∠AOB=120°，∴∠OEB=∠AFO，在△AOF与△BOE中，∵∠OBE=∠OAF，∠OEB=∠AFO，OA=OB，∴△AOF≌△BEO，∴OE=OF，∴∠OFG=（180°﹣∠EOF）=30°，∴∠AFO=∠GFO，过O作OG⊥EF于G，∴∠OAF=∠OGF=90°，在△AOF与△OGF中，∵∠OAF=∠OGF，∠AFO=∠GFO，OF=OF，∴△AOF≌△GOF，∴OG=OA，∴EF是⊙O的切线．

【题型】解答题
【结束】
25

【题目】如图，在平面直角坐标系中，O为原点，四边形ABCO是矩形，点A，C的坐标分别是A（0，2）和C（2，0），点D是对角线AC上一动点（不与A，C重合），连结BD，作DE⊥DB，交x轴于点E，以线段DE，DB为邻边作矩形BDEF．

（1）填空：点B的坐标为　　；

（2）是否存在这样的点D，使得△DEC是等腰三角形？若存在，请求出AD的长度；若不存在，请说明理由；

（3）①求证：；

②设AD=x，矩形BDEF的面积为y，求y关于x的函数关系式（可利用①的结论），并求出y的最小值．

查看答案和解析>>

科目：初中数学 来源： 题型：

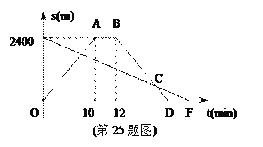
【题目】小明从家骑自行车出发，沿一条直路到相距2400m的邮局办事，小明出发的同时，他的爸爸以96m/min速度从邮局同一条道路步行回家，小明在邮局停留2min后沿原路以原速返回，设他们出发后经过t min时，小明与家之间的距离为s1m，小明爸爸与家之间的距离为s2 m，图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象。

（1）求s2与t之间的函数关系式；

（2）小明从家出发，经过多长时间在返回途中追上爸爸？这时他们距离家还有多远？