
分析 根据[x)表示大于x的最小整数,可得[3)=4,[-1.2)=-1,据此对各说法进行判断即可.
解答 解:①根据[x)表示大于x的最小整数可得,[-2.1)+[4.3)=-2+5=3,故①正确;
②根据[x)表示大于x的最小整数可得,当x是整数时,[x)-x的最大值是1,故②正确;
③根据[x)表示大于x的最小整数可得,[x)>x,故[x)-x的最小值不等于0,故③错误;
最小值是0;
④根据[x)表示大于x的最小整数可得,当x为0.5的奇数倍时,[x)-x=0.5成立,故④正确.
故答案为:①②④.
点评 本题主要考查了有理数大小的比较,解题的关键是运用[x)表示大于x的最小整数进行计算求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
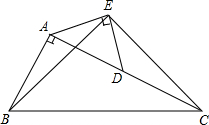 已知:如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,以AD为斜边在△ABC外作等腰直角三角形AED,连结BE、EC.试猜想线段BE和EC有何关系,并证明你的猜想.
已知:如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,以AD为斜边在△ABC外作等腰直角三角形AED,连结BE、EC.试猜想线段BE和EC有何关系,并证明你的猜想.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com