练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，以点O为旋转中心，将∠1按顺时针方向旋转110°得到∠2，若∠1=40°，则∠2的余角为


    1. A.
      140°
    2. B.
      70°
    3. C.
      50°
    4. D.
      150°
    C
    分析：由于∠1按顺时针方向旋转110°得到∠2，根据旋转的性质得到∠2=∠1=40°，然后利用余角的定义求∠2的余角．
    解答：∵∠1按顺时针方向旋转110°得到∠2，
    ∴∠2=∠1=40°，
    ∴∠2的余角=90°-40°=50°．
    故选C．
    点评：本题考查了旋转的性质：旋转前后两图形全等，即对应角相等，对应线段相等．也考查了余角的定义．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    23、在下面的网格图中按要求画出图形，并回答问题：
    （1）先画出△ABC向下平移5格后的△A1B1C1，再画出△ABC以点O为旋转中心，沿顺时针方向旋转90°后的△A2B2C2；
    （2）如图，以点O为原点建立平面直角坐标系，试写出点A2，B1的坐标．

    查看答案和解析>>

    科目：初中数学 来源：解题升级　　解题快速反应一典通　　九年级级数学 题型：044

    如图，在正方形ABCD中，E是AD的中点，F是BA延长线上的一点，AF＝AB．(1)求证：△ABE≌△ADF．(2)阅读下面的材料：

    如图，把△ABC沿直线BC平行移动线段BC的长度，可以变到△FCD的位置：

    如图，以BC为轴把△ABC翻折，可以变到△DBC的位置；

    如图，以点A为旋转中心，把△ABC旋转，可以变到△AED的位置．

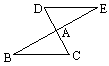
    像这样，其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的，这种只改变位置，不改变形状大小的变换叫做三角形的全等变换．

    回答下列问题：①在下图中可以通过平行移动、翻折、旋转中的哪一种方法，使△ABE变到△ADF的位置？②指出下图中线段BE与DF之间的关系．

    查看答案和解析>>

    科目：初中数学 来源：2012年北师大版初中数学八年级上3.5它们是怎样变过来的练习卷（解析版） 题型：解答题

    如图①，在正方形ABCD中，E是AD的中点，F是BA延长线上的一点，AF=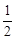AB，

    （1）求证：△ABE≌△ADF.

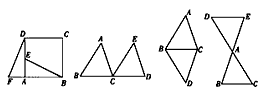
    （2）阅读下列材料：如图②，把△ABC沿直线平移线段BC的长度，可以变到△ECD的位置；如图③，以BC为轴把△ABC翻折180°，可以变到△DBC的位置；如图④，以点A为中心，把△ABC旋转180°，可以变到△AED的位置，像这样其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的，这种只改变位置，不改变形状大小的图形变换，叫做三角形的全等变换.

          图①               图②                  图③           图④

    请回答下列问题：

    （1）在图①中，可以通过平移、翻折、旋转中的哪一种方法，使△ABE变到△ADF的位置？

    （2）指出图①中线段BE与DF之间的关系.

     

    查看答案和解析>>

    科目：初中数学 来源：同步题 题型：解答题

    如图所示①，在正方形ABCD中，E是AD的中点，F是BA延长线上的一点，AF=。

         ①                 ②                ③          ④
    （1）求证：△ABE≌△ADF；
    （2）阅读下面材料：
    如图②，把△ABC沿直线BC平行移动线段BC的长度，可以变到△ECD的位置；
    如图③，以BC为轴把△ABC翻折180°，可以变到△DBC的位置；
    如图④，以点A为中心，把△ABC旋转180°，可以变到△AED的位置。
    像这样，其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的，这种只改变位置，不改变形状大小的图形变换，叫做三角形的全等变换。
    回答下列问题：
    ①在图①中，可以通过平行移动、翻折、旋转中的哪一种方法，使△ABE变到△ADF的位置？
    ②指出图①中线段BE与DF之间的关系。

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年云南省曲靖市麒麟区沿江二中九年级（上）期末数学试卷（解析版） 题型：解答题

    在下面的网格图中按要求画出图形，并回答问题：
    （1）先画出△ABC向下平移5格后的△A1B1C1，再画出△ABC以点O为旋转中心，沿顺时针方向旋转90°后的△A2B2C2；
    （2）如图，以点O为原点建立平面直角坐标系，试写出点A2，B1的坐标．

    查看答案和解析>>

    同步练习册答案