练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．如图，在方格纸中，线段AB的两个端点都在小方格的格点上，AB=5，请找到一个格点P，连结PA，PB，使得△PAB为等腰三角形（请画出两种，若所画三角形全等，则视为一种）．

    分析 根据AB=5，运用勾股定理作出AP=5或BP=5，即可得到△PAB为等腰三角形．

    解答 解：如图所示，△PAB即为所求．

    点评 本题主要考查了等腰三角形的判定，以及应用与设计作图的运用，解题时注意：等腰三角形是一个轴对称图形，它的定义既作为性质，又可作为判定办法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．计算：
    （1）（-1）3-$\frac{1}{4}$×[2-（-3）2]
    （2）-5m2n+4mn2-2mn+6m2n+3mn
    （3）5（3a2b-ab2）-（ab2+3a2b），其中a=-$\frac{1}{2}$，b=$\frac{1}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

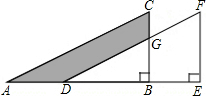    11．如图，将直角三角形ABC沿AB方向平移AD长的距离得到直角三角形DEF，已知BE=5，EF=8，CG=3．则图中阴影部分面积$\frac{65}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．分式$\frac{5x+6}{2x-3}$的值不可能等于$\frac{5}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．先化简，再求值：$\frac{{x}^{2}-9}{{x}^{2}+6x+9}$-$\frac{x}{x+3}$，其中x=4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．计算：
    （1）$\sqrt{18}$×$\sqrt{\frac{1}{2}}$÷$\sqrt{3}$
    （2）（$\sqrt{3}$+$\sqrt{2}$）2×（$\sqrt{5}$-2$\sqrt{6}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．某公司为了扩大经营，决定购进6台机器用于生产某种活塞，现有甲、乙两种机器共选择，其中每种机器的价格和每台机器日生产活塞的数量如下表所示：
    甲乙
    价格/（万元/台）75
    每台日产量/个10060
    经过预算，本次购买机器所耗资金不能超过34万元．
    （1）按该公司要求可以有几种购买方案？
    （2）若该公司购进的6台机器的日生产能力不能低于380个，那么为了节约资金应选择哪种购买方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

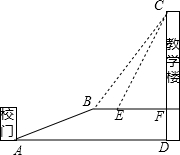    9．重庆市是著名的山城，重庆建筑多因地制宜，某中学依山而建，校门A处，有一斜坡AB，斜坡AB的坡度i=5：12，从A点沿斜坡行走了19.5米到达坡顶B处，在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°，离B点5米远的E处有一花台，在花台E处仰望C的仰角∠CEF=63.4°，CF的延长线交校门处的水平面于点D，则DC的长（　　）（参考数据：tan53°≈$\frac{4}{3}$，cos53°≈$\frac{3}{5}$，tan63.4°≈2，sin63.4°≈$\frac{9}{10}$）
    A．25B．27.5C．30D．32.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．下列各曲线中，不能表示y是x的函数的是（　　）
    A．B．C．D．

    查看答案和解析>>

    同步练习册答案