��1����������y=ax
2-2ax+c֪���Գ��� x=1��
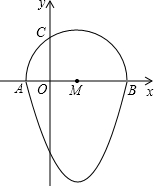
���M��������1��0����
�ߵ�A��B���ڵ�M�Գƣ���A��-1��0����M��1��0��
��B��3��0������Բ�İ뾶 r=AM=BM=2��
����CM����Rt��OCM��CM=r=2��OM=1��OC=
=
=
���� C��0��
����
�ʴ𰸣�B��3��0����C��0��
������ԲM�İ뾶Ϊ2��
��2����������y=ax
2-2ax+c����A��-1��0������
a+2a+c=0��c=-3a
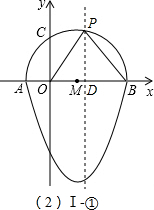
�������ߣ�y=ax
2-2ax-3a��
����P�ڰ�Բ��ʱ��
�ٵ�P��ֱ�Ƕ��㣬����ͼ��ͼ��-�٣���
����OBP�ǵ���ֱ�������Σ���ô��P����OB���д����ϣ��� AD=BD=PD=
��
��Rt��OPD��OP=2��OD=
���� PD=
=
��
��
�߶�PD����ǰ�����ì�ܣ��������������������
�ڵ�O��ֱ�Ƕ��㣻
�ɣ�1��֪��OC=
��OB������������Ҳ��������
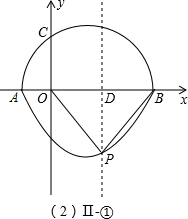
��P����������ʱ��
�ٵ�P��ֱ�Ƕ��㣬����ͼ��ͼ��-�٣���
����OPB�ǵ���ֱ�������Σ��� OD=BD=PD=
���� P��
��-
����
����P���������y=ax
2-2ax-3a����
a����
��
2-2a��
-3a=-
��
��ã�a=
��
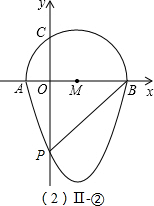
�ڵ�O��ֱ�Ƕ��㣬��ô��P��Ϊ��������y��Ľ��㣨��ͼ��-�ڣ���
����OPBΪ����ֱ�������Σ��� OP=OB=3���� P��0��-3����
ͬ�٣���ã�a=1��
���ϣ���P��0��-3��ʱ��a=1����P��
��-
��ʱ��a=
��
��3������ֱ��y=x-
��������y=ax
2-2ax-3a����
x-
=ax
2-2ax-3a��
���ã�ax
2-��2a+1��x-3a+
=0
���=��2a+1��
2-4a��-3a+
��=16a
2-10a+1=0��
��ã�a=
��a=
��
�����������������ߵĽ���ʽΪ��y=
x
2-x-
��y=
x
2-
x-
��
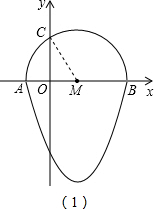

 �������ߣ�y=ax2-2ax-3a��
�������ߣ�y=ax2-2ax-3a��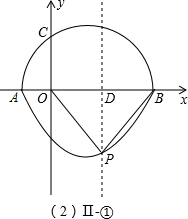 ��P����������ʱ��
��P����������ʱ�� ���ϣ���P��0��-3��ʱ��a=1����P��
���ϣ���P��0��-3��ʱ��a=1����P��







