
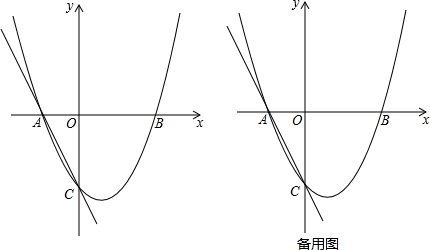
分析 (1)根据与x轴的两个交点A、B的坐标,设出二次函数交点式解析式y=a(x+1)(x-2),然后把点C的坐标代入计算求出a的值,即可得到二次函数解析式;
(2)设OP=x,然后表示出PC、PA的长度,在Rt△POC中,利用勾股定理列式,然后解方程即可;
(3)①根据相似三角形对应角相等可得∠MCH=∠CAO,然后分(i)点H在点C下方时,利用同位角相等,两直线平行判定CM∥x轴,从而得到点M的纵坐标与点C的纵坐标相同,是-2,代入抛物线解析式计算即可;(ii)点H在点C上方时,根据(2)的结论,点M为直线PC与抛物线的另一交点,求出直线PC的解析式,与抛物线的解析式联立求解即可得到点M的坐标;
②在x轴上取一点D,过点D作DE⊥AC于点E,可以证明△AED和△AOC相似,根据相似三角形对应边成比例列式求解即可得到AD的长度,然后分点D在点A的左边与右边两种情况求出OD的长度,从而得到点D的坐标,再作直线DM∥AC,然后求出直线DM的解析式,与抛物线解析式联立求解即可得到点M的坐标.
解答 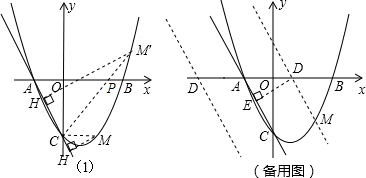 解:(1)设该二次函数的解析式为:y=a(x+1)(x-2),
解:(1)设该二次函数的解析式为:y=a(x+1)(x-2),
将x=0,y=-2代入,得-2=a(0+1)(0-2),
解得a=1,∴抛物线的解析式为y=(x+1)(x-2),即y=x2-x-2;
(2)设OP=x,则PC=PA=x+1,在Rt△POC中,
由勾股定理,得x2+22=(x+1)2,解得,x=$\frac{3}{2}$,即OP=$\frac{3}{2}$;
(3)①∵△CHM∽△AOC,
∴∠MCH=∠CAO,
(i)如图1,当H在点C下方时,
∵∠OAC+∠OCA=90°,∠MCH=∠OAC
∴∠OCA+∠MCH=90°
∴∠OCM=90°=∠AOC
∴CM∥x轴
∴yM=-2,
∴x2-x-2=-2,
解得x1=0(舍去),x2=1,
∴M(1,-2),
(ii)如图1,当H在点C上方时,
∵∠MCH=∠CAO,
∴PA=PC,由(2)得,M′为直线CP与抛物线的另一交点,
设直线CM′的解析式为y=kx-2,把P($\frac{3}{2}$,0)的坐标代入,得$\frac{3}{2}$k-2=0,
解得k=$\frac{4}{3}$,
∴y=$\frac{4}{3}$x-2,由$\frac{4}{3}$x-2=x2-x-2,
解得x1=0(舍去),x2=$\frac{7}{3}$,此时y=$\frac{4}{3}$×$\frac{7}{3}$-2=$\frac{10}{9}$,
∴M′($\frac{7}{3}$,$\frac{10}{9}$),
②在x轴上取一点D,如图(备用图),过点D作DE⊥AC于点E,使DE=$\frac{{6\sqrt{5}}}{5}$,
在Rt△AOC中,AC=$\sqrt{A{O}^{2}+C{O}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∵∠COA=∠DEA=90°,∠OAC=∠EAD,
∴△AED∽△AOC,
∴$\frac{AD}{AC}$=$\frac{DE}{OC}$,
解得AD=3,
∴D(2,0)或D(-4,0).
过点D作DM∥AC,交抛物线于M,如图(备用图)
则直线DM的解析式为:y=-2x+4或y=-2x-8,
当-2x-8=x2-x-2时,即x2+x+6=0,方程无实数根,
当-2x+4=x2-x-2时,即x2+x-6=0,解得x1=2,x2=-3,
∴点M的坐标为(2,0)或(-3,10).
点评 本题是对二次函数的综合考查,主要利用了待定系数法求二次函数解析式,勾股定理,相似三角形的性质,两函数图象交点的求解方法,综合性较强,难度较大,要注意分情况讨论求解.


科目:初中数学 来源: 题型:选择题
| A. | 这300名考生是总体的一个样本 | B. | 近5000多名考生是总体 | ||
| C. | 每位考生的数学成绩是个体 | D. | 300名考生是样本容量 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
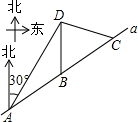 如图,我市云台山景区内一条笔直的公路a经过三个景点A、B、C,现在市政府决定开发风景优美的景点D.经测量景点D位于景点A的北偏东30°方向12km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上.已知AB=4$\sqrt{3}$km.
如图,我市云台山景区内一条笔直的公路a经过三个景点A、B、C,现在市政府决定开发风景优美的景点D.经测量景点D位于景点A的北偏东30°方向12km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上.已知AB=4$\sqrt{3}$km.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 材料1:
材料1:| 恩格尔系数 大于或等于60% | 恩格尔系数 在50%~60%之间 | 恩格尔系数 在40%~50%之间 | 恩格尔系数 在30%~40%之间 | 恩格尔系数 小于30% |
| 绝对贫困 | 温 饱 | 小 康 | 富 裕 | 最富裕 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,BC=4,E、F分别是AB、AC上的点,且EF∥BC,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q,当3CQ=CE时,EP+BP=8.
如图,在△ABC中,BC=4,E、F分别是AB、AC上的点,且EF∥BC,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q,当3CQ=CE时,EP+BP=8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com