
分析 设其中较大的一段的长为xcm(x≥10),则另一段的长为(24-x)cm,根据两个正方形的面积之和为12cm2建立方程求出其解即可.
解答 解:设其中较大的一段的长为xcm(x≥12),则另一段的长为(24-x)cm.
则两个小正方形的边长分别为$\frac{1}{4}$x cm和$\frac{1}{4}$(24-x)cm
∵两正方形面积之差为12cm2,
∴($\frac{1}{4}$x)2-[$\frac{1}{4}$(24-x)]2=12,
解得x=16cm.则另一段长为24-16=8cm.
∴两段铁丝中较长的为16cm.
故答案是:16.
点评 本题考查了正方形的面积公式的运用,列一元二次方程解实际问题的运用,一元二次方程的解法的运用,解答时两个正方形的面积之和为12cm2建立方程是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 100,120 | B. | 120,110 | C. | 110,120 | D. | 120,120 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
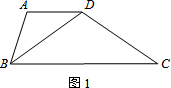 我们把有一组邻边相等,一组对边平行但不相等的四边形称作“准菱形”.
我们把有一组邻边相等,一组对边平行但不相等的四边形称作“准菱形”.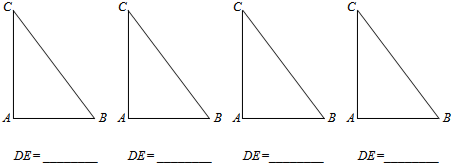
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com