
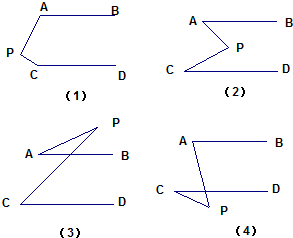
 28、已知,AB∥CD,分别探讨四个图形中∠APC,∠PAB,∠PCD的关系.
28、已知,AB∥CD,分别探讨四个图形中∠APC,∠PAB,∠PCD的关系.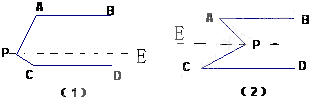 解:(1)图1,∠A+∠P+∠C=360°,
解:(1)图1,∠A+∠P+∠C=360°,

 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
(本小题满分1 0分)
如图,已知线段AB∥CD,AD与B C相交于点K,E是线段AD上一动点。

1.(1)若BK=![]() KC,求
KC,求![]() 的值;
的值;
2.(2)连接BE,若BE平分∠ABC,则当AE= ![]() AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当AE=
AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当AE=![]() AD(n>2),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.
AD(n>2),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.
查看答案和解析>>
科目:初中数学 来源:2012届四川省营山县九年级上学期期末考试数学卷 题型:解答题
(本小题满分1 0分)
如图,已知线段AB∥CD,AD与B C相交于点K,E是线段AD上一动点。
【小题1】(1)若BK= KC,求
KC,求 的值;
的值;
【小题2】(2)连接BE,若BE平分∠ABC,则当AE=  AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当AE=
AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当AE= AD (n>2),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.
AD (n>2),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏扬州江都大桥镇花荡中学九年级上第一次月考数学试卷(解析版) 题型:解答题
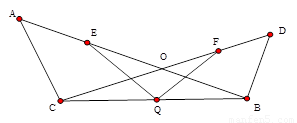
如图,已知:AB,CD交于点O,CA=CO,BO=BD,点Q是BC的中点,点E,F分别是OA,OD的中点,连接QE,QF,试探讨QE,QF的大小关系,并说明理由
查看答案和解析>>
科目:初中数学 来源:2012年四川省营山县九年级上学期期末考试数学卷 题型:解答题
(本小题满分1 0分)
如图,已知线段AB∥CD,AD与B C相交于点K,E是线段AD上一动点。

1.(1)若BK= KC,求
KC,求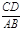 的值;
的值;
2.(2)连接BE,若BE平分∠ABC,则当AE= 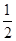 AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当AE=
AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当AE= AD
(n>2),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.
AD
(n>2),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com