
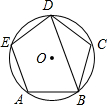
 如图,正五边形ABCDE为内接于⊙O的,则∠ABD=72°.
如图,正五边形ABCDE为内接于⊙O的,则∠ABD=72°.  应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:解答题
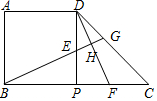 ABPD是一个边长为1的正方形,△DPC是一个直角边长为1的等腰直角三角形,把正方形ABPD和△DPC拼成一个如图所示的直角梯形,E、F分别为线段DP、CP上两个动点(不与D、P、C重合),且DE=CF=x,BE的延长线分别交DF、DC于H、G.
ABPD是一个边长为1的正方形,△DPC是一个直角边长为1的等腰直角三角形,把正方形ABPD和△DPC拼成一个如图所示的直角梯形,E、F分别为线段DP、CP上两个动点(不与D、P、C重合),且DE=CF=x,BE的延长线分别交DF、DC于H、G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
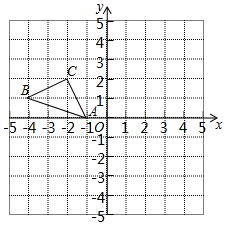 正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | -$\frac{1}{2}$ | C. | -2 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9cm | B. | 5cm | C. | 6cm或5cm | D. | 5cm或9cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 数量范围(千克) | 0~50 | 50以上~150的部分 | 150以上~250的部分 | 250以上的部分 |
| 价格(元) | 零售价的90% | 零售价的80% | 零售价的70% | 零售价的60% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com