Question

解不等式

x-1

2

-

x

4

≤-1并把解集在数轴上表示出来．求满足不等式组

x-2(x+1)≥-1 x-1 3 - 2x+3 2 ＜ 1 x-6

的整数x的值．

Answer 1

分析：将不等式两边同乘以4，然后再根据移项、系数化为1求出不等式的解，并把它在数轴上表示出来；由题意知将不等式组中的不等式的解集根据移项、合并同类项、系数化为1分别解出来，然后再根据解不等式组解集的口诀：大小小大中间找，来求出不等式组解，从而写出其整数解．

解答：解：将不等式

x-1

2

-

x

4

≤-1两边同乘以4得
2（x-1）-x≤-4，
∴2x-2-x≤-4，
∴x≤-2，
解集在数轴上表示如下图：

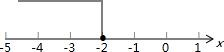
由不等式x-2（x+1）≥-1去括号得，
∴x-2x-2≥-1，
∴-x≥1，
解得x≤-1，
由不等式

x-1

3

-

2x+3

2

＜

1

x-6

，
当x＞6时，不等式两边同乘以6（x-6）得
（2x-2）（x-6）-（6x+9）（x-6）＜6，
∴4x²-13x-60＞0，
解得x＞

13+ 1129

8

或x＜

13- 1129

8

，
∴x＞6，
当x＜6时，不等式两边同乘以6（x-6）得
2x-2-（6x+9）＞6，
解得

13- 1129

8

＜x＜

13+ 1129

8

∴

13- 1129

8

＜x＜

13+ 1129

8

∴不等式组的解集为：

13- 1129

8

＜x≤-1，
∴不等式的整数解为：-2，-1．

点评：此题主要考查了一元一次不等式组解集的求法，利用不等式组解集的口诀：同大取大，同小取小，大小小大中间找，大大小小找不到（无解），来求解；另外把不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．