
【题目】如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E、G、H分别在矩形ABCD的边AB、CD、DA上,AH=2. 
(1)若DG=6,求AE的长;
(2)若DG=2,求证:四边形EFGH是正方形.
【答案】
(1)解:∵AD=6,AH=2
∴DH=AD﹣AH=4
∵四边形ABCD是矩形
∴∠A=∠D=90°
∴在Rt△DHG中,HG2=DH2+DG2
在Rt△AEH中,HE2=AH2+AE2
∵四边形EFGH是菱形
∴HG=HE
∴DH2+DG2=AH2+AE2
即42+62=22+AE2
∴AE= ![]() =4
=4 ![]()
(2)证明:∵AH=2,DG=2,
∴AH=DG,
∵四边形EFGH是菱形,
∴HG=HE,
在Rt△DHG和Rt△AEH中,
![]() ,
,
∴Rt△DHG≌Rt△AEH(HL),
∴∠DHG=∠AEH,
∵∠AEH+∠AHE=90°,
∴∠DHG+∠AHE=90°,
∴∠GHE=90°,
∵四边形EFGH是菱形,
∴四边形EFGH是正方形
【解析】(1)先根据矩形的性质,利用勾股定理列出表达式:HG2=DH2+DG2 , HE2=AH2+AE2 , 再根据菱形的性质,得到等式DH2+DG2=AH2+AE2 , 最后计算AE的长;(2)先根据已知条件,用HL判定Rt△DHG≌Rt△AEH,得到∠DHG=∠AEH,因为∠AEH+∠AHE=90°,∠DHG+∠AHE=90°,可得菱形的一个角为90°,进而判定该菱形为正方形.
【考点精析】掌握菱形的性质和矩形的性质是解答本题的根本,需要知道菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;矩形的四个角都是直角,矩形的对角线相等.


科目:初中数学 来源: 题型:
【题目】若一元二次方程ax2+bx+c=0中的a=3,b=0,c=﹣2,则这个一元二次方程是( )
A.3x2﹣2=0B.3x2+2=0C.3x2+x=0D.3x2﹣x=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频数分布直方图如下:

(1)直接写出a的值,并补全频数分布直方图.
分组 | 频数 | 频率 |
49.5~59.5 | 0.08 | |
59.5~69.5 | 0.12 | |
69.5~79.5 | 20 | |
79.5~89.5 | 32 | |
89.5~100.5 | a |
(2)若成绩在80分以上(含80分)为优秀,求这次参赛的学生中成绩为优秀的约为多少人?
(3)若这组被抽查的学生成绩的中位数是80分,请直接写出被抽查的学生中得分为80分的至少有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年博鳌亚洲论坛年会开幕大会上,中国全面阐述了亚洲合作政策,并特别强调要推进“一带一路”的建设,中国将出资400亿美元设丝路基金.用科学记数法表示400亿美元为美元.
查看答案和解析>>
科目:初中数学 来源: 题型:
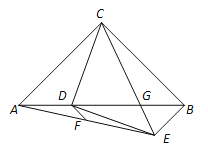
【题目】如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D为边AB上一点,CD绕点D顺时针旋转90°至DE,CE交AB于点G.已知AD=8,BG=6,点F是AE的中点,连接DF,求线段DF的长___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大米包装袋上(25±0.1)kg的标识表示此袋大米的重量为( )
A. 24.9kg﹣25.1kgB. 24.9kg
C. 25.1kgD. 25kg
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,∠ACB=30°,BC=8,以BC为边,在△ABC外作等边△BCD,点E为BC中点,连接AE并延长交CD于点F.
(1)求证:四边形ABDF是平行四边形;
(2)如图2,将图1中的ABCD折叠,使点D和点A重合,折痕为GH,求CG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com