
【题目】如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在图①,图②中已画出线段AB,在图③中已画出点A.按下列要

求画图:
(1)在图①中,以格点为顶点,AB为一边画一个等腰三角形ABC;
(2)在图②中,以格点为顶点,AB为一边画一个正方形;
(3)在图③中,以点A为一个顶点,另外三个顶点也在格点上,画一个面积最大的正方
形,这个正方形的面积= .
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
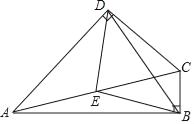
【题目】已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,点E是AC的中点.(1)求证:△BED是等腰三角形:
(2)当∠BCD=_____°时,△BED是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明调查了全班本学期阅读课外书的情况,并根据统计数据,绘制如下的频率分布折线图和扇形统计图。
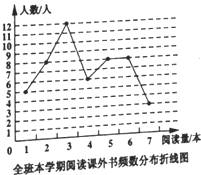
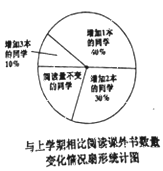
根据以上信息,回答下列问题:
①这个班共有__________ 名学生,本学期阅读量5本的有________ 人
②这个班本学期阅读量的中位数是_______ 本,众数是 ______ 本;
③求全班本学期比上学期每名同学的平均阅读量增加了多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程组解应用题:某学校在筹建数学实验室过程中,准备购进一批桌椅,现有三种桌椅可供选择:甲种每套150元,乙种每套210元,丙种每套250元。若该学校同时购买其中两种不同型号的桌椅50套,恰好花费了9000元,则共有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
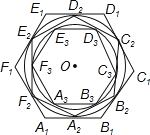
【题目】如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD的边AB=3,AD=2,将此矩形置入直角坐标系中,使AB在x 轴上,点C 在直线y=x-2上.
(1)求矩形各顶点坐标;
(2)若直线y=x-2与y轴交于点E,抛物线过E、A、B三点,求抛物线的关系式;
(3)判断上述抛物线的顶点是否落在矩形ABCD内部,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索:
(x-1)(x+1)=x2-1, (x-1)(x2+x+1)=x3-1,
(x-1)(x3+x2+x+1)=x4-1, (x-1)(x4+x3+x2+x+1)=x5-1,
……
(1)试写出第五个等式;
(2)试求26+25+24+23+22+2+1的值;
(3)判断22 017+22 016+22 015+…+22+2+1的值的个位数字是几.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是﹣4,点C在数轴上表示的数是4,若线段AB以3个单位长度/秒的速度向右匀速运动,同时线段CD以1个单位长度/秒的速度向左匀速运动.
![]()
(1)问运动多少秒时BC=2(单位长度)?
(2)线段AB与线段CD从开始相遇到完全离开共经过多长时间?
(3)P是线段AB上一点,当B点运动到线段CD上,且点P不在线段CD上时,是否存在关系式BD﹣AP=3PC.若存在,求线段PD的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com