
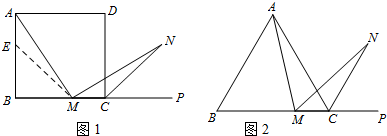
分析 (1)要证明AM=MN,可证AM与MN所在的三角形全等,为此,可在AB上取一点E,使AE=CM,连接ME,利用ASA即可证明△AEM≌△MCN,然后根据全等三角形的对应边成比例得出AM=MN.
(2)同(1),要证明AM=MN,可证AM与MN所在的三角形全等,为此,可在AB上取一点E,使AE=CM,连接ME,利用ASA即可证明△AEM≌△MCN,然后根据全等三角形的对应边成比例得出AM=MN.
(3)由(1)(2)可知,∠AMN等于它所在的正多边形的一个内角即等于$\frac{(n-2)•180°}{n}$时,结论AM=MN仍然成立.
解答 (1)证明:在边AB上截取AE=MC,连接ME.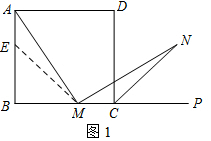
∵正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAB=∠MAE,
BE=AB-AE=BC-MC=BM,
∴∠BEM=45°,∴∠AEM=135°.
∵N是∠DCP的平分线上一点,
∴∠NCP=45°,∴∠MCN=135°.
在△AEM与△MCN中,
$\left\{\begin{array}{l}{∠MAE=∠NMC}\\{AE=MC}\\{∠AEM=∠MCN}\end{array}\right.$,
∴△AEM≌△MCN(ASA),
∴AM=MN.
(2)解:结论AM=MN还成立.
证明:在边AB上截取AE=MC,连接ME.
在正△ABC中,∠B=∠BCA=60°,AB=BC.
∴∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAE,
BE=AB-AE=BC-MC=BM,
∴∠BEM=60°,∴∠AEM=120°.
∵N是∠ACP的平分线上一点,
∴∠ACN=60°,∴∠MCN=120°.
在△AEM与△MCN中,
$\left\{\begin{array}{l}{∠MAE=∠NMC}\\{AE=MC}\\{∠AEM=∠MCN}\end{array}\right.$,
∴△AEM≌△MCN(ASA),
∴AM=MN.
(3)解:若将(1)中的“正方形ABCD”改为“正n边形ABCD…X,则当∠AMN=[$\frac{(n-2)•180}{n}$]°时,结论AM=MN仍然成立.
故答案为[$\frac{(n-2)•180}{n}$].
点评 本题综合考查了正方形、等边三角形的性质及全等三角形的判定和性质,同时考查了学生的归纳能力及分析、解决问题的能力,解题的关键是学会添加辅助线,构造全等三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | 三个加数全为0 | B. | 至少有两个加数是负数 | ||
| C. | 至少有一个加数是正数 | D. | 至少有两个加数是正数 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
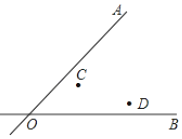 如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要在∠AOB内部修建一个货站P,使货站P到两条公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹,写出结论)
如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要在∠AOB内部修建一个货站P,使货站P到两条公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹,写出结论)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com