
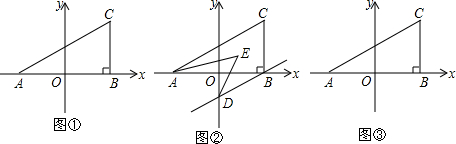
分析 (1)根据非负数的性质得a+2=0,b-2=0,解得a=-2,b=2,则A(-2,0),C(2,2),B(2,0),然后根据三角形面积公式计算S△ABC;
(2)如图③,AC交y轴于Q,先确定Q(0,1),设P(0,t),利用三角形面积公式和S△PAC=S△APQ+S△CPQ=S△ABC得到$\frac{1}{2}$•|t-1|•2+$\frac{1}{2}$•|t-1|•2=4,然后解方程求出t即可得到P点坐标;
(3)作EM∥AC,如图②,则AC∥EM∥BD,根据平行线的性质得∠CAE=∠AEM,∠BDE=∠DEM,则∠AED=∠CAE+∠BDE,而∠CAE=$\frac{1}{2}$∠CAB,∠BDE=$\frac{1}{2}$∠ODB,所以∠AED=$\frac{1}{2}$(∠CAB+∠ODB),而由AC∥BD得到∠CAB=∠OBD,于是∠CAB+∠ODB=∠OBD+∠ODB=90°,则∠AED=45°.
解答 解:(1)∵(a+2)2+$\sqrt{b-2}$=0,
∴a+2=0,b-2=0,解得a=-2,b=2,
∴A(-2,0),C(2,2),
∵CB⊥x轴,
∴B(2,0),
∴S△ABC=$\frac{1}{2}$×(2+2)×2=4;
(2)存在.
如图③,AC交y轴于Q,则Q(0,1),
设P(0,t),
∵S△PAC=S△APQ+S△CPQ=S△ABC,
∴$\frac{1}{2}$•|t-1|•2+$\frac{1}{2}$•|t-1|•2=4,解得t=3或t=-1,
∴P点坐标为(0,3),(0,-1);
(3)作EM∥AC,如图②,
∵AC∥BD,
∴AC∥EM∥BD,
∴∠CAE=∠AEM,∠BDE=∠DEM,
∴∠AED=∠CAE+∠BDE,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠CAE=$\frac{1}{2}$∠CAB,∠BDE=$\frac{1}{2}$∠ODB,
∴∠AED=$\frac{1}{2}$(∠CAB+∠ODB),
∵AC∥BD,
∴∠CAB=∠OBD,
∴∠CAB+∠ODB=∠OBD+∠ODB=90°,
∴∠AED=$\frac{1}{2}$×90°=45°.
点评 本题考查了坐标与图形性质:利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系.也考查了平行线的性质和三角形面积公式.


科目:初中数学 来源: 题型:解答题
 如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:填空题
对于二次函数y = x2-2mx-3,有下列结论:①它的图象与x轴有两个交点;②如果将它的图象向左平移3个单位 后过原点,则m=1;③如果当x = 2时的函数值与x = 8时的函数值相等,则m=5.其中一定正确的结论是____________.(把你认为正确结论的序号都填上)
后过原点,则m=1;③如果当x = 2时的函数值与x = 8时的函数值相等,则m=5.其中一定正确的结论是____________.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:填空题
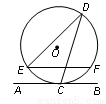
如图,直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长度为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,∠ABC、∠ACB的平分线相交于点F,过点F作DE∥BC交AB于D,交AC于E.若AB=9cm,AC=8cm,则△ADE的周长是多少?
如图所示,∠ABC、∠ACB的平分线相交于点F,过点F作DE∥BC交AB于D,交AC于E.若AB=9cm,AC=8cm,则△ADE的周长是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com