
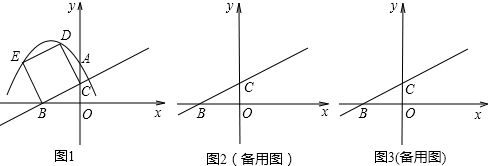
如图1,在直角坐标系中,O是坐标原点,点A在y轴正半轴上,二次函数y=ax2+ x
+c的图象F交x轴于B、C两点,交y轴于M点,其中B(-3,0),M(0,-1)。已知AM=BC。
x
+c的图象F交x轴于B、C两点,交y轴于M点,其中B(-3,0),M(0,-1)。已知AM=BC。
(1)求二次函数的解析式;
(2)证明:在抛物线F上存在点D,使A、B、C、D四点连接而成的四边形恰好是平行四边形,并请求出直线BD的解析式;
(3)在(2)的条件下,设直线l过D且分别交直线BA、BC于不同的P、Q两点,AC、BD相交于N。
①若直线l⊥BD,如图1所示,试求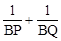 的值;
的值;
②若l为满足条件的任意直线。如图2所示,①中的结论还成立吗?若成立,证明你的猜想;若不成立,请举出反例。

解:(1)∵二次函数y=ax2+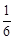 x
+c的图象经过点B(-3,0),M(0,-1),
x
+c的图象经过点B(-3,0),M(0,-1),
∴  ,解得
,解得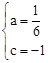 。
。
∴二次函数的解析式为: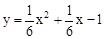 。
。
(2)证明:在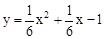 中,令y=0,得
中,令y=0,得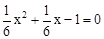 ,解得x1=-3,x2=2。
,解得x1=-3,x2=2。
∴C(2,0),∴BC=5。
令x=0,得y=-1,∴M(0,-1),OM=1。
又AM=BC,∴OA=AM-OM=4。∴A(0,4)。
设AD∥x轴,交抛物线于点D,如图1所示,
则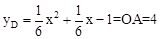 ,解得x1=5,x2=-6(位于第二象限,舍去)。
,解得x1=5,x2=-6(位于第二象限,舍去)。
∴D点坐标为(5,4)。∴AD=BC=5。
又∵AD∥BC,∴四边形ABCD为平行四边形,即在抛物线F上存在点D,使A、B、C、D四点连接而成的四边形恰好是平行四边形。
设直线BD解析式为:y=kx+b,∵B(-3,0),D(5,4),
∴ 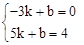 ,解得:
,解得: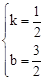 。
。
∴直线BD解析式为: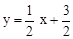 。
。
(3)在Rt△AOB中,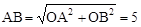 ,
,
又AD=BC=5,∴▱ABCD是菱形。
①若直线l⊥BD,如图1所示,
∵四边形ABCD是菱形,∴AC⊥BD。∴AC∥直线l。∴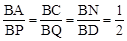 。
。
∵BA=BC=5,∴BP=BQ=10。
∴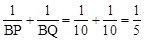 。
。
②若l为满足条件的任意直线,如图2所示,此时①中的结论依然成立,理由如下:
∵AD∥BC,CD∥AB,∴△PAD∽△DCQ。∴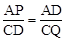 。
。
∴AP•CQ=AD•CD=5×5=25。
∴
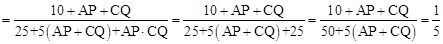 。
。
【解析】(1)利用待定系数法求出二次函数的解析式。
(2)首先求出D点的坐标,可得AD=BC且AD∥BC,所以四边形ABCD是平行四边形;再根据B、D点的坐标,利用待定系数法求出直线BD的解析式。
(3)本问的关键是判定平行四边形ABCD是菱形。
①推出AC∥直线l,从而根据平行线间的比例线段关系,求出BP、CQ的长度,计算出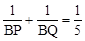 。
。
②判定△PAD∽△DCQ,得到AP•CQ=25,利用这个关系式对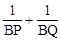 进行分式的化简求值,结论为
进行分式的化简求值,结论为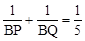 不变。
不变。


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
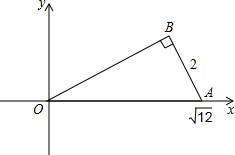 已知在Rt△OAB中,∠B=90°,AO=
已知在Rt△OAB中,∠B=90°,AO=| 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| ||||
| a+12 |

查看答案和解析>>
科目:初中数学 来源: 题型:
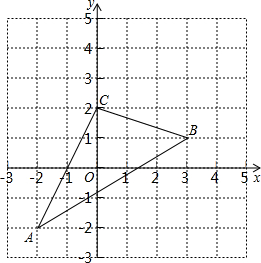 如图,△ABC在直角坐标系中,
如图,△ABC在直角坐标系中,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com