
分析 仿照例子,将3换成m,设S=1+m+m2+m3+m4+…+m2016(m≠0且m≠1),则有mS=m+m2+m3+m4+…+m2017,二者做差后两边同时除以m-1,即可得出结论.
解答 解:设S=1+m+m2+m3+m4+…+m2016(m≠0且m≠1)①,
将①×m得:mS=m+m2+m3+m4+…+m2017②,
由②-①得:mS-S=m2017-1,即S=$\frac{{m}^{2017}-1}{m-1}$,
∴1+m+m2+m3+m4+…+m2016=$\frac{{m}^{2017}-1}{m-1}$(m≠0且m≠1).
故答案为:$\frac{{m}^{2017}-1}{m-1}$(m≠0且m≠1).
点评 本题考查了规律型中的数字的变化类,解题的关键是仿照例子计算1+m+m2+m3+m4+…+m2016.本题属于基础题,难度不大,本题其实是等比数列的求和公式,但初中未接触过该方面的知识,需要借助于错位相减法来求出结论,此题中尤其要注意m的取值范围.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:选择题
| A. | 32017-1 | B. | 32018-1 | C. | $\frac{{3}^{2017}-1}{4}$ | D. | $\frac{{3}^{2017}-1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 抛物线L:y=ax2+bx+c(a≠0,a、b、c为常数)的顶点为原点,且经过点A(2$\sqrt{a}$,$\frac{1}{4}$),直线y=kx+1与y轴交于点F,与抛物线L交于B(x1,y1)、C(x2,y2)两点(其中x1<x2).有直线l:y=-1,垂足为M,连接AF.
抛物线L:y=ax2+bx+c(a≠0,a、b、c为常数)的顶点为原点,且经过点A(2$\sqrt{a}$,$\frac{1}{4}$),直线y=kx+1与y轴交于点F,与抛物线L交于B(x1,y1)、C(x2,y2)两点(其中x1<x2).有直线l:y=-1,垂足为M,连接AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
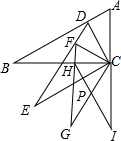 如图,Rt△ABC中,∠B=30°,∠ACB=90°,CD⊥AB交AB于D,以CD为较短的直角边向△CDB的同侧作Rt△DEC,满足∠E=30°,∠DCE=90°,再用同样的方法作Rt△FGC,∠FCG=90°,继续用同样的方法作Rt△HIC,∠HCI=90°.若AC=a,求CI的长.
如图,Rt△ABC中,∠B=30°,∠ACB=90°,CD⊥AB交AB于D,以CD为较短的直角边向△CDB的同侧作Rt△DEC,满足∠E=30°,∠DCE=90°,再用同样的方法作Rt△FGC,∠FCG=90°,继续用同样的方法作Rt△HIC,∠HCI=90°.若AC=a,求CI的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com