
分析 将63代入操作程序,只需要3次后变为2,设这个最大正整数为m,则$\sqrt{m}$,从而求得这个最大的数.
解答 解:63$\stackrel{第1次}{→}$[$\sqrt{63}$)=8$\stackrel{第2次}{→}$[$\sqrt{8}$)=3$\stackrel{第3次}{→}$[$\sqrt{3}$)=2,
设这个最大正整数为m,则m$\stackrel{第1次}{→}$[$\sqrt{m}$)=63,
∴$\sqrt{m}$<63.
∴m<3969.
∴m的最大正整数值为3968.
故答案为:3968.
点评 此题主要考查了估算无理数的大小,确定出经过3次变化后值为2的最大正整数值是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
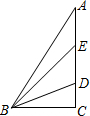 如图,在△ABC中∠C=90°,D、E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是( )
如图,在△ABC中∠C=90°,D、E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是( )| A. | BE是△ABD的中线 | B. | BD是△BCE的角平分线 | ||
| C. | ∠ABE=∠EBD=∠DBC | D. | BC是△ABE的高 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com