
分析 已知该抛物线与坐标轴的交点,所以设该抛物线解析式为两点式:y=a(x-1)(x+1),然后把点A的坐标代入求得a的值;结合抛物线的增减性来求y的取值范围.
解答 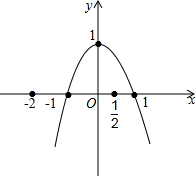 解:∵二次函数y=ax2+bx+c的图象经过B(-1,0),C(1,0),
解:∵二次函数y=ax2+bx+c的图象经过B(-1,0),C(1,0),
∴设该抛物线解析式为两点式:y=a(x-1)(x+1),
把A(0,1)代入,得
a(0-1)(0+1)=1,
解得a=-1.
故该函数关系式为:y=-(x-1)(x+1),或y=-x2+1.
如图所示,当x=-2时,y最小=-22+1=-3.
当x=1时,y最大=1.
故y的取值范围为:-3≤y≤1.
故答案是:y=-(x-1)(x+1)或y=-x2+1;-3≤y≤1.
点评 本题考查了待定系数法求二次函数的解析式,解题时,注意“数形结合”数学思想的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
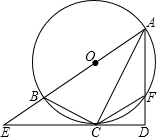 如图,已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接BC、CF、AC.
如图,已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接BC、CF、AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
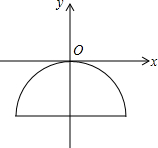 如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度是16米,跨度是46米.
如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度是16米,跨度是46米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线y=kx+5与x轴交于点A,与y交于点B,与抛物线y=ax2+bx交于点C、D.已知点C坐标为(1,7),点C横坐标为5.
如图,在平面直角坐标系中,直线y=kx+5与x轴交于点A,与y交于点B,与抛物线y=ax2+bx交于点C、D.已知点C坐标为(1,7),点C横坐标为5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
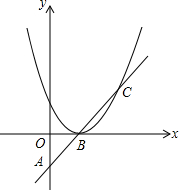 如图,抛物线y=ax2沿着x轴移动,与直线AB相交于B,C两点,若B(1,0)且OA=OB,AB=BC.
如图,抛物线y=ax2沿着x轴移动,与直线AB相交于B,C两点,若B(1,0)且OA=OB,AB=BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com