
 某校王老师组织九(1)班同学开展数学活动,某天带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A的仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高AB.(结果用根号表示)
某校王老师组织九(1)班同学开展数学活动,某天带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A的仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高AB.(结果用根号表示) 分析 延长AD交BC的延长线于G,作DH⊥BG于H,根据正弦、余弦的定义求出CH、DH,根据正切的定义求出HG,设AB=xm,根据正切的定义求出BG,结合图形列出方程,解方程即可.
解答 解:延长AD交BC的延长线于G,作DH⊥BG于H,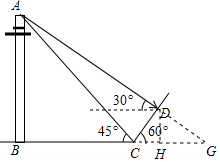
在Rt△DHC中,∠DCH=60°,CD=4,
则CH=CD•cos∠DCH=4×cos60°=2,
DH=CD•sin∠DCH=4×sin60°=$2\sqrt{3}$,
∵DH⊥BG,∠G=30°,
∴HG=$\frac{DH}{tan∠G}$=$\frac{{2\sqrt{3}}}{tan30°}$=6,
∴CG=CH+HG=2+6=8,
设AB=xm,
∵AB⊥BG,∠G=30°,∠BCA=45°,
∴BC=x,BG=$\frac{AB}{tan∠G}=\frac{x}{tan30°}$=$\sqrt{3}$x,
∵BG-BC=CG,
∴$\sqrt{3}$x-x=8,
解得:x=$\frac{8}{{\sqrt{3}-1}}$=4($\sqrt{3}$+1)(m)
答:电线杆的高为x=4($\sqrt{3}$+1)m.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角俯角的等腰、熟记锐角三角函数的定义是解题的关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:填空题
 如图,O是正方形ABCD的中心,M是ABCD内一点,∠DMC=90°,将△DMC绕O点旋转180°后得到△NAB,若MD=3,CM=4,则MN的长为$\sqrt{2}$.
如图,O是正方形ABCD的中心,M是ABCD内一点,∠DMC=90°,将△DMC绕O点旋转180°后得到△NAB,若MD=3,CM=4,则MN的长为$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>$\frac{1}{2}$ | B. | k<$\frac{1}{2}$ | C. | k=$\frac{1}{2}$ | D. | k≤$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
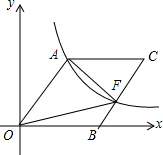 如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,反比例函数y=$\frac{48}{x}$在第一象限内的图象经过点A(6,m),与BC交于点F,则△AOF的面积等于( )
如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,反比例函数y=$\frac{48}{x}$在第一象限内的图象经过点A(6,m),与BC交于点F,则△AOF的面积等于( )| A. | 50 | B. | 40 | C. | 30 | D. | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$>$\sqrt{3}$ | B. | 2<$\sqrt{5}$ | C. | 2$\sqrt{2}$<$\sqrt{5}$ | D. | 0<-$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
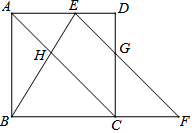 如图,在正方形ABCD中,E是AD边上的动点(与A、D不重合),点F在边BC的延长线上,且AE=CF,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H.
如图,在正方形ABCD中,E是AD边上的动点(与A、D不重合),点F在边BC的延长线上,且AE=CF,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com