
����Ŀ����ͼ�������ߵĽ���ʽΪy����![]() x+5����������x�ύ��A��B���㣨A����B�����ࣩ����y�ύ�ڵ�C�������߶Գ�����ֱ��BC���ڵ�D��
x+5����������x�ύ��A��B���㣨A����B�����ࣩ����y�ύ�ڵ�C�������߶Գ�����ֱ��BC���ڵ�D��
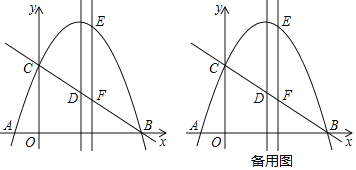
��1��E�����߶�BC�Ϸ���������һ�㣬����E��ֱ��EFƽ����y�ᣬ��BC�ڵ�F�����߶�CD���ȱ��ֲ��䣬��ֱ��BC�ƶ��õ�C'D'�����߶�EF���ʱ����EC'+C'D'+![]() D'B����Сֵ��
D'B����Сֵ��
��2��Q����������һ���㣬���������߶Գ������Ƿ����һ��P�ǡ�APQΪ�ȱ������Σ������ڣ���ֱ��д�������α߳�������������˵�����ɣ�
���𰸡���1��![]() ����2�����ڣ�����Ҫ��ĵȱ������εı߳������ǣ�6
����2�����ڣ�����Ҫ��ĵȱ������εı߳������ǣ�6![]() ��2
��2![]() ��2
��2![]() ��
��
��������
��1�����ݽ���ʽ�ѱ�Ҫ�ĵ�����꼰�߶γ�����������ã���E���������Ϊδ֪������E��F��������֮���ʾEF���ȣ�ͨ���䷽��EF����ֵ��ȡ����ֵʱE�����꣮����C'D'���Ȳ��䣬��˽�EC'ƽ����E'D'��ע���CBO��30�㣬��D'G��OB��G��E'H��OB��H�����ݴ��߶����ԭ������ȷ����ֵ��
��2��ͼ��������������ֱ���й�ͼ��⣮��Q��B�غ�ʱ��Ӧ����ͼ��P��x�Ϸ����·���������������ĵȱ������εı߳���һ���ģ�����AB�ij��������������Q��C�غϣ���ʱ�ĵȱ������α߳�����AC���ȣ���������£�P��ʵ���ǡ�ABC�����ģ��������������Q�ڵ������ޣ�����PQ��PA��PB������Բ�ܽ���Բ�ĽǵĹ�ϵ�ɵá�ABQ��30�㣬���ǿ����BQ����ʽ����BQ����ʽ�������߽���ʽ����������ɽ��Q�����꣬Ȼ���������ľ��빫ʽ���AQ���Ⱦ��Ƕ�Ӧ�ĵȱ������εı߳���
�⣺��1����Ϊy����![]() x2+
x2+![]() x+5����
x+5����![]() ��x��5
��x��5![]() ����x+
����x+![]() ����
����
��A����![]() ��0����B��5
��0����B��5![]() ��0����C��0��5���������߶Գ���Ϊx��
��0����C��0��5���������߶Գ���Ϊx��![]() ��2
��2![]() ��
��
��B��C��������ֱ��BC�Ľ���ʽΪy����![]() x+5��
x+5��
��x��2![]() ����y����
����y����![]() ��2
��2![]() +5��3��
+5��3��
��D��2![]() ��3����
��3����
��CD��C'D'��4��
��E��m����![]() m2+
m2+![]() m+5������F��m����
m+5������F��m����![]() m+5����
m+5����
��EF��yE��yF����![]() m2+
m2+![]() m+5+
m+5+![]() m��5����
m��5����![]() m2+
m2+![]() m����
m����![]() ��m��
��m��![]() ��2+
��2+![]() ��
��
�൱m��![]() ʱ��EFȡ�����ֵ
ʱ��EFȡ�����ֵ![]() ����ʱE��
����ʱE��![]() ��
��![]() ����
����
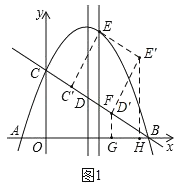
��ͼ1����ƽ���ı���EC'D'E'����EC'��E'D'��E'��![]() ��
��![]() ����
����
��D'G��OB��G��E'H��OB��H��
��tan��CBO��![]() ��
��![]() ��
��![]() �����ԡ�CBO��30�㣬
�����ԡ�CBO��30�㣬
��D'G��![]() D'B��
D'B��
��EC'+C'D'+D'B��C'D'+E'D'+D'G��C'D'+E'H��
���ҽ���E'��D'��G���㹲��ʱ��
EC'+C'D'+![]() D'Bȡ����СֵC'D'+E'H��4+
D'Bȡ����СֵC'D'+E'H��4+![]() ��
��![]() ��
��
��2������ͼ2����APQ�ǵȱ������Σ���ʱQ��B�غϣ�
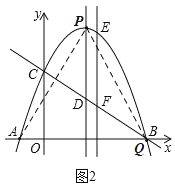
��ȱ������εı߳�ΪAQ��AB��6![]() ��
��
����ͼ3����APQ�ǵȱ������Σ���ʱQ��B�غϣ�P��x���·���

��ȱ������εı߳�ΪAQ��AB��6![]() ��
��
����ͼ4����APQ�ǵȱ������Σ���ʱQ��C�غϣ�P��x���Ϸ���
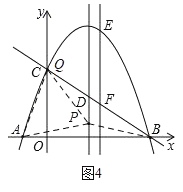
��ȱ������εı߳�ΪAQ��AC��2![]() ��
��
����ͼ5����APQ�ǵȱ������Σ���ʱQ�ڵ������ޣ�P��x���·���
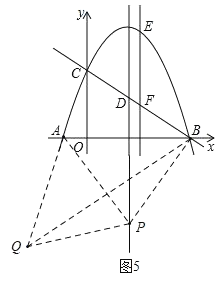
��PA��PB��PQ������A��Q��B��������PΪԲ��PAΪ�뾶ΪԲ���ϣ�
���ABQ��![]() ��APQ��30�㣬
��APQ��30�㣬
��ֱ��BQ�Ľ���ʽΪy��![]() x��5��
x��5��
����������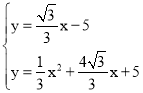 ��
��
���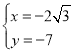 ��
��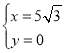 ���ᣩ��
���ᣩ��
��Q������2![]() ����7����
����7����
��AQ��2![]() �����ȱߡ�APQ�ı߳�Ϊ2
�����ȱߡ�APQ�ı߳�Ϊ2![]() ��
��
��������������Ҫ��ĵȱ������εı߳������ǣ�6![]() ��2
��2![]() ��2
��2![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
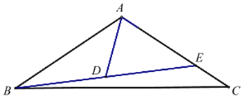
����Ŀ����ͼ����ABC�У�AB=AC��E��AC�ϣ�BD=DE��tan��DAE=3��AD=![]() ��CE=2�����߶�AC�ij�Ϊ__________��
��CE=2�����߶�AC�ij�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�����Ӳ�Ʒר����20Ԫ/���ļ۸�������ij�¿��������������60������������������������
��������(��x��) | �ۼ�(Ԫ) | ��������(��) |
1��x��35 | x+30 | 100��2x |
35��x��60 | 70 | 100��2x |
(1)��������ÿ�������ΪWԪ�����W��x�ĺ�����ϵʽ��
(2)�����������ε���һ����������W���Դﵽ���ֵ�����ֵΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
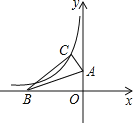
����Ŀ����ͼ����֪��A��0��1����B����3��0��������AB������ABO��AB���ۣ�ʹ��O���C�غϣ��ҵ�Cǡ���ں���y��![]() �ϣ���k��ֵΪ��������
�ϣ���k��ֵΪ��������
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��10��10�հ���18��10���ң�����ʡ������ɽ��312�����Ϻ�����K135��������·�Ͽ��ų�������෭�����3��������2�����ˣ����ܸ��¹�ԭ���������Ϊ���ǣ�������س��ص������������෭������Ҳ�������������������ư�ȫ�Եĵ��ǣ����л�����չ�������ṹ��Ƶİ�ȫ�Խ�����������֪�����㸲ϵ��Խ�ߣ���ȫ��Խǿ�������㸲ϵ����2��5ʱ����Ϊ�ýṹ��ȫ�������������������ȡ�˼ס����������Ժ����������ڽ��Ļ��ѽ���20��������Ŀ�����Ų飬���õ��Ŀ��㸲���ݽ��������������ͷ��������㸲������x��ʾ�����ֳ�6�飺A��0��x��2��5��B��2��5��x��5��0��C��5��0��x��7��5��D��7��5��x��10��0��E��10��0��x��12��5��F��12��5��x��15������������˲�����Ϣ��
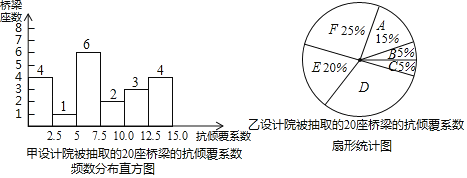
���У������ԺC��Ŀ��㸲ϵ���ǣ�7��7��7��6��7��7��
�����ԺD��Ŀ��㸲ϵ���ǣ�8��8��9��8��8��8��
�ס������Ժ�ֱ𱻳�ȡ��20�������Ŀ��㸲ϵ��ͳ�Ʊ�
���Ժ | �� | �� |
ƽ���� | 7.7 | 8.9 |
���� | a | 8 |
��� | 7 | b |
���� | 19.7 | 18.3 |
����������Ϣ����������⣺
��1������ͳ��ͼ��D����������Ӧ��Բ�Ľ����� ���ȣ�a���� ����b���� ����
��2�������������ݣ��ס����������Ժ���ĸ����Ժ��������ȫ�Ը��ߣ�˵�����ɣ�һ�����ɣ����� ����
��3����ͳ�ƣ�2018����2019�꣬�����Ժ������80�������������Ժ������120�������������2018����2019�������Ժ�IJ���ȫ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���� 10��6 �������������У�ÿ��С�����εı߳���Ϊ 1���߶� AB �Ķ˵� A��B ����С�����εĶ����ϣ�
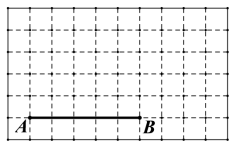
��1����ͼ�л����� AB Ϊһ���ĵ�����ABC���� C ��С�����ζ����ϣ���ABC Ϊ�۽������Σ�����ABC �����Ϊ![]() ��
��
��2����ͼ�л����� AB Ϊб�ߵ�ֱ�������� ABD�� �� D��С�����εĶ����ϣ��� AD>BD��
��3������ CD������ֱ��д���߶� CD �ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() �ύ��
�ύ��![]() ���㣬
���㣬![]() ���Ե�
���Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶��Բ�ϵĶ��㣬
Ϊ�뾶��Բ�ϵĶ��㣬![]() ���߶�
���߶�![]() ���е㣬����
���е㣬����![]() �����߶�
�����߶�![]() ����Сֵ�ǣ� ��
����Сֵ�ǣ� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ijͯװר�����������з��֣�һ��ͯװÿ������Ϊ40Ԫ�������ۼ�Ϊ60Ԫ��ÿ����۳�20����Ϊӭ����˫ʮһ����ר���������ȡ�ʵ��Ľ��۴�ʩ�������������������г����鷢�֣����ÿ��ͯװ����1Ԫ����ôƽ���ɶ��۳�2��![]() ��ÿ��ͯװ����xԪ
��ÿ��ͯװ����xԪ![]() ʱ��ƽ��ÿ���ӯ��yԪ��
ʱ��ƽ��ÿ���ӯ��yԪ��
![]() д��y��x�ĺ�����ϵʽ��
д��y��x�ĺ�����ϵʽ��
![]() ����ר����ÿ��ͯװ���۶���Ԫʱ��ƽ��ÿ��ӯ��400Ԫ��
����ר����ÿ��ͯװ���۶���Ԫʱ��ƽ��ÿ��ӯ��400Ԫ��
![]() ��ר����Ҫ��ƽ��ÿ��ӯ��600Ԫ����������˵�����ɣ�
��ר����Ҫ��ƽ��ÿ��ӯ��600Ԫ����������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�Һ���λ�ڵ���P����ƫ��30�����������100�����A�������ƻ������������У�ȥ��λ�ڵ���P�ı�ƫ��45�������ϵ�B����

��1����B���������P�ж�Զ���������ȷ��0.1���
��2��������һԲ�ΰ�����������Բ��λ������PB�ϣ��������150����ĵ�O����Բ�ΰ�������İ뾶Ϊ60���������������д�����Σ�գ����жϺ��ֵ���B���Ƿ��д�����Σ�գ�������ִ�B�����������������У��Ƿ��д�����Σ�գ���˵�����ɣ����ο����ݣ�![]() ��1.414��
��1.414��![]() ��1.732��
��1.732��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com