
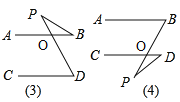
����Ŀ����ͼ(1)��AB��CD�������BPD���B.��D�Ĺ�ϵ��˵�����ɣ�(��ʾ�������ε��ڽǺ͵���180��)
����ջ���д����
�⣺�����BPD+��B+��D=360��
���ɣ�����P��EF��AB��
���B+��BPE=180��______
��AB��CD��EF��AB��
��______��_____��(�������ֱ�߶��͵�����ֱ��ƽ�У���ô������ֱ��Ҳ����ƽ��)
���EPD+______=180��
���B+��BPE+��EPD+��D=360��
���B+��BPD+��D=360��
����������Ľ��ⷽ�����۲�ͼ(2)����֪AB��CD������ͼ�еġ�BPD���B.��D�Ĺ�ϵ����˵�����ɣ�

�۹۲�ͼ(3)��(4)����֪AB��CD��ֱ��д��ͼ�еġ�BPD���B.��D�Ĺ�ϵ����˵�����ɣ�
���𰸡���
��ֱ��ƽ�У�ͬ���ڽǻ�����CD��EF����CDP�ڲ����BPD����B����D�����ɼ������ۣ�3����BPD����B����D����4����BPD����B��D.
��������
�ٹ���P��EF��AB��������ֱ��ƽ�У�ͬ���ڽǻ�����֤�����ۣ�
����ٵķ������ƣ�����P��EP��AB��������ֱ��ƽ�У��ڴ�����ȣ�֤�����ۣ�
�۸���ƽ���ߵ����ʼ���������Ƕ���������⣮
�ٲ����BPD����B����D��360��
���ɣ�����P��EF��AB��
���B����BPE��180�㣨��ֱ��ƽ�У�ͬ���ڽǻ�����
��AB��CD��EF��AB��
��CD��EF�����������ֱ�߶��͵�����ֱ��ƽ�У���ô������ֱ��Ҳ����ƽ�У�
���EPD����CDP��180��
���B����BPE����EPD����D��360��
���B����BPD����D��360��
�����ֱ��ƽ�У�ͬ���ڽǻ�����CD��EF����CDP
�ڲ����BPD����B����D
���ɣ�����P��EP��AB��
���B����BPE����ֱ��ƽ�У�ͬλ����ȣ�
��AB��CD��EF��AB��
��CD��EF�����������ֱ�߶��͵�����ֱ��ƽ�У���ô������ֱ��Ҳ����ƽ�У�
���EPD����D
���BPD����B����D

����ͼ��3����PD��AB����O�㣬
��AB��CD�����D=��AOP��
�ߡ�AOP=��BPD����B��
���BPD����B����D��
����BPD����B����D�Ĺ�ϵΪ��BPD����B����D��
��ͼ��4����PB��CD����O�㣬
��AB��CD�����B=��COP��
�ߡ�COP=��BPD����D��
���BPD����D����B��
����BPD����B����D�Ĺ�ϵΪ��BPD����B��D.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ı���ABCD�У�![]() ��
��![]() ��
��![]() ��
��
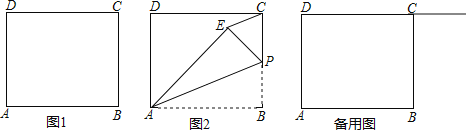
![]() Ϊ��BC��һ�㣬��
Ϊ��BC��һ�㣬��![]() ��ֱ��AP������
��ֱ��AP������![]() ��λ��
��λ��![]() ��B���ڵ�E��
��B���ڵ�E��![]()
![]() ��ͼ1������E����CD����ʱ�����ó߹���ͼ����ͼ1����������������ͼ��
��ͼ1������E����CD����ʱ�����ó߹���ͼ����ͼ1����������������ͼ��![]() ��д������������ͼ�ۼ�����2BǦ�ʼӴּӺ�
��д������������ͼ�ۼ�����2BǦ�ʼӴּӺ�![]() ��ֱ��д����ʱ
��ֱ��д����ʱ![]() ______��
______��
![]() ��ͼ2������PΪBC�ߵ��е㣬����CE����CE��AP�к�λ�ù�ϵ����˵�����ɣ�
��ͼ2������PΪBC�ߵ��е㣬����CE����CE��AP�к�λ�ù�ϵ����˵�����ɣ�
![]() ��QΪ����DC�ϵ�һ�����㣬��
��QΪ����DC�ϵ�һ�����㣬��![]() ��AQ���ۣ���Dǡ������ֱ��BQ�ϵĵ�
��AQ���ۣ���Dǡ������ֱ��BQ�ϵĵ�![]() ������
������![]() ______��
______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���1����39��Ԫ����A��B������Ʒ���������������6��Ԫ�����ǵĽ��ۺ��ۼ����±���![]() ������
������![]() ��������
��������![]() ������
������![]()
��Ʒ�۸� | A | B |
���� | 1200 | 1000 |
�ۼ� | 1350 | 1200 |
(1)���̳���1�ι���A��B������Ʒ�����ټ���
(2)�̳���2����ԭ���۹���A��B������Ʒ������A��Ʒ�ļ������䣬������B��Ʒ�ļ����ǵ�1�ε�2����A��Ʒ��ԭ�ۼ����ۣ���B��Ʒ��ԭ�ۼ۴������ۣ���������Ʒ������ϣ�Ҫʹ�õ�2�ξ�Ӫ�����������54000Ԫ����B����Ʒ�Ǵ������۵ģ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��˼������������⣺
ԭ�⣺��ͼ1���ı���ABCD��![]() ��
��![]() ��
��![]() ��P��Q�ֱ����ı���ABCD�ı�BC��CD�ϣ�
��P��Q�ֱ����ı���ABCD�ı�BC��CD�ϣ�![]() ����֤��
����֤��![]() ��
��
![]() ______��
______��
![]() С������̽������ͼ2������P��Q��λ�����⻯��ʹ
С������̽������ͼ2������P��Q��λ�����⻯��ʹ![]() ��
��![]() ����E��F�ֱ��ڱ�BC��CD�ϣ���ʱ��֤����
����E��F�ֱ��ڱ�BC��CD�ϣ���ʱ��֤����![]() ����֤����ʱ���ۣ�
����֤����ʱ���ۣ�
![]() ������
������![]() ����������ԭ���У����Ӹ����ߣ���ͼ3����
����������ԭ���У����Ӹ����ߣ���ͼ3����![]() ��
��![]() ������ֱ�ΪE��F������������ԭ���֤����
������ֱ�ΪE��F������������ԭ���֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����գ��������֤�����̣�����������ע�����ɣ�
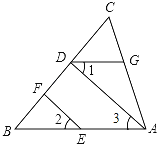
��ͼ����֪��CGD=��CAB����1=��2����֤����ADF+��CFE=180��
֤�����ߡ�CGD=��CAB
��DG��______(______)
���1=______(______)
�ߡ�1=��2
���2=��3(______)
��EF��______(______)
���ADF+��CFE=180��(______)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Rt��ABC��б�߳�Ϊ5��б���ϵĸ�Ϊ2�������ֱ�������η�����ƽ��ֱ������ϵ�У�ʹ��б��AB��x���غϣ�����OA��OB����ֱ�Ƕ���C����y���������ϣ���ͼ1����
��1�����߶�OA,OB�ij��;�����A��B��C�������ߵĹ�ϵʽ��
��2����ͼ2����D������Ϊ��2��0������P��m��n���Ǹ��������ϵ�һ�����㣨����m��0��n��0��������DP��BC�ڵ�E��
�ٵ���BDE�ǵ���������ʱ��ֱ��д����ʱ��E�����꣮
��������CD��CP����ͼ3������CDP�Ƿ��������������У������CDP���������ʹ�ʱ��P�����ꣻ��û�У���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������P��x��y�����������㷽����![]()
��1�����P�����꣨�ú�m��n��ʽ�ӱ�ʾ����
��2������P�ڵ������ޣ��ҷ���Ҫ�������mֻ����������n��ȡֵ��Χ��
��3������P��x��ľ���Ϊ5����y��ľ���Ϊ4����m��n��ֵ��ֱ��д��������ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=��![]() x+4��x�ᡢy��ֱ��ڵ�A����B����D��y��ĸ������ϣ�������DAB��ֱ��AD�۵�����Bǡ������x���������ϵĵ�C����
x+4��x�ᡢy��ֱ��ڵ�A����B����D��y��ĸ������ϣ�������DAB��ֱ��AD�۵�����Bǡ������x���������ϵĵ�C����
��1����AB�ij��͵�C�����ꣻ
��2����ֱ��CD�Ľ���ʽ��
��3��y�����Ƿ����һ��P��ʹ��S��PAB=![]() �������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ABC�У�A����2��1����B����4����2����C����1����3������A��B��C������ABCƽ��֮��õ���ͼ������C�Ķ�Ӧ��C��������Ϊ��4��1����
��1��A����B��.���������ֱ�ΪA����������������B����������������
��2����������ABCƽ��֮���ͼ����A��B��C����
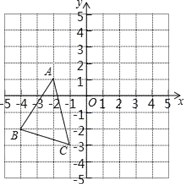
��3������A��B��C���������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com