
【题目】如图所示,在平面内,给定不在同一直线上的点![]() ,
,![]() ,
,![]() ,射线
,射线![]() 是
是![]() 的平分线,点
的平分线,点![]() 到点
到点![]() ,
,![]() ,
,![]() 的距离均等于
的距离均等于![]() (
(![]() 为常数),到点
为常数),到点![]() 的距离等于
的距离等于![]() 的所有点组成图形
的所有点组成图形![]() ,图形
,图形![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)过点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,作
,作![]() 于点
于点![]() ,延长
,延长![]() 交图形
交图形![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,求直线
,求直线![]() 与图形
与图形![]() 的公共点个数.
的公共点个数.
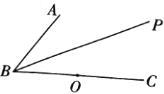
【答案】(1)证明见解析;(2)1个.
【解析】
(1)利用圆的定义得到图形G为△ABC的外接圆⊙O,由∠ABD=∠CBD可得到弧AD等于弧CD,从而圆周角、弧、弦的关系得到AD=CD;
(2)如图,证明CD=CM,则可得到BC垂直平分DM,利用垂径定理得到BC为直径,再证明OD⊥DE,从而可判断DE为⊙O的切线,于是得到直线DE与图形G的公共点个数.
(1)证明:∵到点O的距离等于a的所有点组成图形G,
∴图形G为△ABC的外接圆⊙O,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴![]() ,
,
∴AD=CD;
(2)如图,
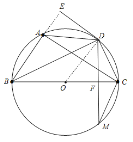
∵AD=CM,AD=CD,
∴CD=CM,
∵DM⊥BC,
∴BC垂直平分DM,
∴BC为直径,
∴∠BAC=90°,
∵![]() ,
,
∴OD⊥AC,
∴OD∥AB,
∵DE⊥AB,
∴OD⊥DE,
∴DE为⊙O的切线,
∴直线DE与图形G的公共点个数为1.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
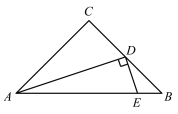
【题目】如图,在△ABC中,AC = BC,∠C=90°,点D是BC的中点,DE⊥AD交BC于点E.若AC =1,则△BDE的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△P1OA1,△P2A1A2,△P3A2A3,…,是等腰直角三角形,点P1,P2,P3,…,在反比例函数y=![]() 的图象上,斜边OA1,A1A2,A2A3,…都在x轴上,则点A3的坐标是_____.
的图象上,斜边OA1,A1A2,A2A3,…都在x轴上,则点A3的坐标是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,B的坐标分别为(-2,3)和(1,3),抛物线y=ax2+bx+c(a<0)的 顶点在线段AB上运动时,形状保持不变,且与x轴交于C,D两点(C在D的左侧),给出下列结论:①c<3;②当x<-3时,y随x的增大而增大;③若点D的横坐标最大值为5,则点C的横坐标最小值为-5;④当四边形ACDB为平行四边形时,a=![]() .其中正确的是( )
.其中正确的是( )
A. ②④ B. ②③ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C是⊙O上的三个点,点D在BC的延长线上.有如下四个结论:①在∠ABC所对的弧上存在一点E,使得∠BCE=∠DCE;②在∠ABC所对的弧上存在一点E,使得∠BAE=∠AEC;③在∠ABC所对的弧上存在一点E,使得EO平分∠AEC;④在∠ABC所对的弧上任意取一点E(不与点A,C重合) ,∠DCE=∠ABO +∠AEO均成立.上述结论中,所有正确结论的序号是( )

A. ①②③ B. ①③④ C. ②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l:y=x+b与x轴交于点A(﹣2,0),与y轴交于点B.双曲线y![]() 与直线l交于P,Q两点,其中点P的纵坐标大于点Q的纵坐标
与直线l交于P,Q两点,其中点P的纵坐标大于点Q的纵坐标
(1)求点B的坐标;
(2)当点P的横坐标为2时,求k的值;
(3)连接PO,记△POB的面积为S.若![]() ,结合函数图象,直接写出k的取值范围.
,结合函数图象,直接写出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
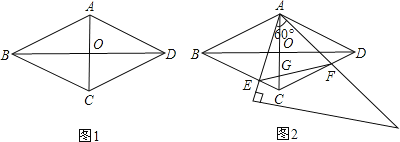
【题目】如图1,在菱形ABCD中,AC=2,BD=2 3 ,AC,BD相交于点O.
(1)求边AB的长;
(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G.
①判断△AEF是哪一种特殊三角形,并说明理由;
②旋转过程中,当点E为边BC的四等分点时(BE>CE),求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司的午餐采用自助的形式,并倡导员工“适度取餐,减少浪费”该公司共有10个部门,且各部门的人数相同.为了解午餐的浪费情况,从这10个部门中随机抽取了![]() 两个部门,进行了连续四周(20个工作日)的调查,得到这两个部门每天午餐浪费饭菜的重量,以下简称“每日餐余重量”(单位:千克),并对这些数据进行了整理、描述和分析.下面给出了部分信息.
两个部门,进行了连续四周(20个工作日)的调查,得到这两个部门每天午餐浪费饭菜的重量,以下简称“每日餐余重量”(单位:千克),并对这些数据进行了整理、描述和分析.下面给出了部分信息.![]() .
.![]() 部门每日餐余重量的频数分布直方图如下(数据分成6组:
部门每日餐余重量的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ):
):
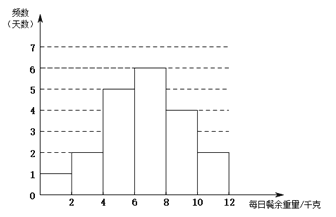
![]() .
.![]() 部门每日餐余重量在
部门每日餐余重量在![]() 这一组的是:6.1 6.6 7.0 7.0 7.0 7.8
这一组的是:6.1 6.6 7.0 7.0 7.0 7.8
![]() .
.![]() 部门每日餐余重量如下:1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
部门每日餐余重量如下:1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
![]() .
. ![]() 两个部门这20个工作日每日餐余重量的平均数、中位数、众数如下:
两个部门这20个工作日每日餐余重量的平均数、中位数、众数如下:
部门 | 平均数 | 中位数 | 众数 |
| 6.4 | | 7.0 |
| 6.6 | 7.2 | |
根据以上信息,回答下列问题:
(1)写出表![]() 中的值;
中的值;
(2)在![]() 这两个部门中,“适度取餐,减少浪费”做得较好的部门是________(填“
这两个部门中,“适度取餐,减少浪费”做得较好的部门是________(填“![]() ”或“
”或“![]() ”),理由是____________;
”),理由是____________;
(3)结合![]() 这两个部门每日餐余重量的数据,估计该公司(10个部门)一年(按240个工作日计算)的餐余总重量.
这两个部门每日餐余重量的数据,估计该公司(10个部门)一年(按240个工作日计算)的餐余总重量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com