
【题目】如图,△ABC是等边三角形,点D在AC上,点E在BC的延长线上,且BD=DE. 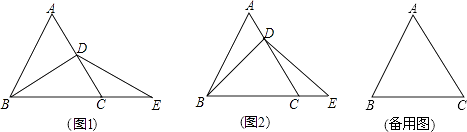
(1)若点D是AC的中点,如图1,求证:AD=CE.
(2)若点D不是AC的中点,如图2,试判断AD与CE的数量关系,并证明你的结论:(提示:过点D作DF∥BC,交AB于点F.)
(3)若点D在线段AC的延长线上,(2)中的结论是否仍成立?如果成立,给予证明;如果不成立,请说明理由.
【答案】
(1)证明:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,AB=AC=BC,
∵D为AC中点,
∴∠DBC=30°,AD=DC,
∵BD=DE,
∴∠E=∠DBC=30°
∵∠ACB=∠E+∠CDE,
∴∠CDE=30°=∠E,
∴CD=CE,
∵AD=DC,
∴AD=CE;
(2)证明:成立,
如图2,过D作DF∥BC,交AB于F,

则∠ADF=∠ACB=60°,
∵∠A=60°,
∴△AFD是等边三角形,
∴AD=DF=AF,∠AFD=60°,
∴∠BFD=∠DCE=180°﹣60°=120°,
∵DF∥BC,
∴∠FDB=∠DBE=∠E,
在△BFD和△DCE中
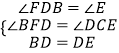
∴△BFD≌△DCE,
∴CE=DF=AD,
即AD=CE.
(3)证明:(2)中的结论仍成立,
如图3,过点D作DP∥BC,交AB的延长线于点P,
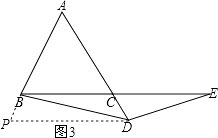
∵△ABC是等边三角形,
∴△APD也是等边三角形,
∴AP=PD=AD,∠APD=∠ABC=∠ACB=∠PDC=60°,
∵DB=DE,
∴∠DBC=∠DEC,
∵DP∥BC,
∴∠PDB=∠CBD,
∴∠PDB=∠DEC,
在△BPD和△DCE中,

∴△BPD≌△DCE,
∴PD=CE,
∴AD=CE.
【解析】(1)求出∠E=∠CDE,推出CD=CE,根据等腰三角形性质求出AD=DC,即可得出答案;(2)过D作DF∥BC,交AB于F,证△BFD≌△DCE,推出DF=CE,证△ADF是等边三角形,推出AD=DF,即可得出答案.(3)(2)中的结论仍成立,如图3,过点D作DP∥BC,交AB的延长线于点P,证明△BPD≌△DCE,得到PD=CE,即可得到AD=CE.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)求证:BE=CF;
(2)如果AB=8,AC=6,求AE、BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明到离家2.1千米的学校参加八年级联欢会,到学校时发现演出道具还放在家中,此时距联欢会开始还有42分钟,于是他立即步行(匀速)回家,在家拿道具用了1分钟,然后立即骑自行车(匀速)返回学校,已知李明骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍。
(1)李明步行的速度(单位:米/分)是多少?
(2)李明能否在联欢会开始前赶到学校?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场经营的某品牌童装,4月的销售额为20000元,为扩大销量,5月份商场对这种童装打9折销售,结果销量增加了50件,销售额增加了7000元.
(1)求该童装4月份的销售单价;
(2)若4月份销售这种童装获利8000元,6月全月商场进行“六一儿童节”促销活动.童装在4月售价的基础上一律打8折销售,若该童装的成本不变,则销量至少为多少件,才能保证6月的利润比4月的利润至少增长25%?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,以CD为边作等边三角形CDE,BE与AC相交于点M,则∠AMD的度数是( )
A.75°
B.60°
C.54°
D.67.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 20 | 30 |
根据图标提供的信息,下列结论错误的是( )

A. 这次被调查的学生人数为200人 B. 扇形统计图中E部分扇形的圆心角为72°
C. 被调查的学生中最想选F的人数为35人 D. 被调查的学生中最想选D的有55人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句:①有一边对应相等的两个直角三角形全等;②一般三角形具有的性质,直角三角形都具有;③有两边相等的两直角三角形全等;④两直角三角形的斜边为5cm,一条直角边都为3cm,则这两个直角三角形必全等.其中正确的有________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣kx+k﹣1=0.
(1)求证:此一元二次方程恒有实数根.
(2)无论k为何值,该方程有一根为定值,请求出此方程的定值根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com