
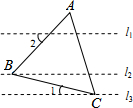
 如图,直线l1∥l2∥l3,等边△ABC的顶点B、C分别在直线l2、l3上,若边BC与直线l3的夹角∠1=25°,则边AB与直线l1的夹角∠2=35°.
如图,直线l1∥l2∥l3,等边△ABC的顶点B、C分别在直线l2、l3上,若边BC与直线l3的夹角∠1=25°,则边AB与直线l1的夹角∠2=35°.  冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:解答题
 在2014年某市初中生毕业体育测试时,一名学生推铅球,已知铅球所经过的路线为抛物线的一部分,建立如图所示的坐标系,由此回答:该同学的成绩是多少?
在2014年某市初中生毕业体育测试时,一名学生推铅球,已知铅球所经过的路线为抛物线的一部分,建立如图所示的坐标系,由此回答:该同学的成绩是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在A、B两处之间要修一条笔直的公路,从A地测得公路走向是北偏东46°,公司要求A、B两地同时开工,并保证若干天后公路准确接通.
如图,在A、B两处之间要修一条笔直的公路,从A地测得公路走向是北偏东46°,公司要求A、B两地同时开工,并保证若干天后公路准确接通.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:| t(秒) | 0 | 0.16 | 0.2 | 0.4 | 0.6 | 0.64 | 0.8 | … |
| x(米) | 0 | 0.4 | 0.5 | 1 | 1.5 | 1.6 | 2 | … |
| y(米) | 0.25 | 0.378 | 0.4 | 0.45 | 0.4 | 0.378 | 0.25 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com