
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬”ĻACB£½45”ć£®µćD£ØÓėµćB”¢C²»ÖŲŗĻ£©ĪŖÉäĻßBCÉĻŅ»¶Æµć£¬Į¬½ÓAD£¬ŅŌADĪŖŅ»±ßĒŅŌŚADµÄÓŅ²ą×÷Õż·½ŠĪADEF£®
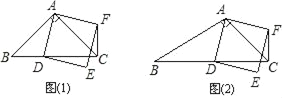
£Ø1£©Čē¹ūAB£½AC£®ČēĶ¼¢Ł£¬ĒŅµćDŌŚĻ߶ĪBCÉĻŌĖ¶Æ£®ŹŌÅŠ¶ĻĻ߶ĪCFÓėBDÖ®¼äµÄĪ»ÖĆ¹ŲĻµ£¬²¢Ö¤Ć÷ÄćµÄ½įĀŪ£®
£Ø2£©Čē¹ūAB”ŁAC£¬ČēĶ¼¢Ś£¬ĒŅµćDŌŚĻ߶ĪBCÉĻŌĖ¶Æ£®£Ø1£©ÖŠ½įĀŪŹĒ·ń³ÉĮ¢£¬ĪŖŹ²Ć“£æ
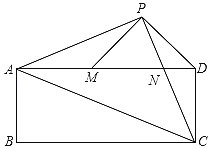
£Ø3£©ČōÕż·½ŠĪADEFµÄ±ßDEĖłŌŚÖ±ĻßÓėĻ߶ĪCFĖłŌŚÖ±ĻßĻą½»ÓŚµćP£¬ÉčAC£½4![]() £¬BC£½3£¬CD£½x£¬ĒóĻ߶ĪCPµÄ³¤£®£ØÓĆŗ¬xµÄŹ½×Ó±ķŹ¾£©
£¬BC£½3£¬CD£½x£¬ĒóĻ߶ĪCPµÄ³¤£®£ØÓĆŗ¬xµÄŹ½×Ó±ķŹ¾£©
”¾“š°ø”æ£Ø1£©CFÓėBDĪ»ÖĆ¹ŲĻµŹĒ“¹Ö±,ĄķÓɼū½āĪö£»£Ø2£©AB”ŁACŹ±£¬CF”ĶBDµÄ½įĀŪ³ÉĮ¢£¬ĄķÓɼū½āĪö£»£Ø3£©¼ū½āĪö
”¾½āĪö”æ
£Ø1£©ÓÉ”ĻACB=45”ć£¬AB=AC£¬µĆ”ĻABD=”ĻACB=45”ć£»æɵƔĻBAC=90”ć£¬ÓÉÕż·½ŠĪADEF£¬æɵƔĻDAF=90”ć£¬AD=AF£¬”ĻDAF=”ĻDAC+”ĻCAF£»”ĻBAC=”ĻBAD+”ĻDAC£»µĆ”ĻCAF=”ĻBAD£®æÉÖ¤”÷DAB”Õ”÷FAC£ØSAS£©£¬µĆ”ĻACF=”ĻABD=45”ć£¬µĆ”ĻBCF=”ĻACB+”ĻACF=90”ć£®¼“CF”ĶBD£®
£Ø2£©¹żµćA×÷AG”ĶAC½»BCÓŚµćG£¬æÉµĆ³öAC=AG£¬Ņ×Ö¤£ŗ”÷GAD”Õ”÷CAF£¬ĖłŅŌ”ĻACF=”ĻAGD=45”ć£¬”ĻBCF=”ĻACB+”ĻACF=90”ć£®¼“CF”ĶBD£®
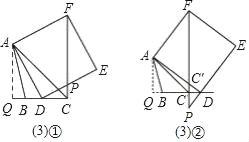
£Ø3£©ČōÕż·½ŠĪADEFµÄ±ßDEĖłŌŚÖ±ĻßÓėĻ߶ĪCFĖłŌŚÖ±ĻßĻą½»ÓŚµćP£¬ÉčAC=4![]() £¬BC=3£¬CD=x£¬ĒóĻ߶ĪCPµÄ³¤£®æ¼ĀĒµćDµÄĪ»ÖĆ£¬·ÖĮ½ÖÖĒéæöČ„½ā“š£®¢ŁµćDŌŚĻ߶ĪBCÉĻŌĖ¶Æ£¬ŅŃÖŖ”ĻBCA=45”ć£¬æÉĒó³öAQ=CQ=4£®¼“DQ=4-x£¬Ņ×Ö¤”÷AQD”×”÷DCP£¬ŌŁøł¾ŻĻąĖĘČż½ĒŠĪµÄŠŌÖŹĒó½āĪŹĢā£®¢ŚµćDŌŚĻ߶ĪBCŃÓ³¤ĻßÉĻŌĖ¶ÆŹ±£¬ÓÉ”ĻBCA=45”ć£¬æÉĒó³öAQ=CQ=4£¬ŌņDQ=4+x£®¹żA×÷AQ”ĶBC½»CBŃÓ³¤ĻßÓŚµćQ£¬Ōņ”÷AGD”×”÷ACF£¬µĆCF”ĶBD£¬ÓÉ”÷AQD”×”÷DCP£¬µĆŌŁøł¾ŻĻąĖĘČż½ĒŠĪµÄŠŌÖŹĒó½āĪŹĢā£®
£¬BC=3£¬CD=x£¬ĒóĻ߶ĪCPµÄ³¤£®æ¼ĀĒµćDµÄĪ»ÖĆ£¬·ÖĮ½ÖÖĒéæöČ„½ā“š£®¢ŁµćDŌŚĻ߶ĪBCÉĻŌĖ¶Æ£¬ŅŃÖŖ”ĻBCA=45”ć£¬æÉĒó³öAQ=CQ=4£®¼“DQ=4-x£¬Ņ×Ö¤”÷AQD”×”÷DCP£¬ŌŁøł¾ŻĻąĖĘČż½ĒŠĪµÄŠŌÖŹĒó½āĪŹĢā£®¢ŚµćDŌŚĻ߶ĪBCŃÓ³¤ĻßÉĻŌĖ¶ÆŹ±£¬ÓÉ”ĻBCA=45”ć£¬æÉĒó³öAQ=CQ=4£¬ŌņDQ=4+x£®¹żA×÷AQ”ĶBC½»CBŃÓ³¤ĻßÓŚµćQ£¬Ōņ”÷AGD”×”÷ACF£¬µĆCF”ĶBD£¬ÓÉ”÷AQD”×”÷DCP£¬µĆŌŁøł¾ŻĻąĖĘČż½ĒŠĪµÄŠŌÖŹĒó½āĪŹĢā£®
£Ø1£©CFÓėBDĪ»ÖĆ¹ŲĻµŹĒ“¹Ö±£»
Ö¤Ć÷ČēĻĀ£ŗ
”ßAB=AC£¬”ĻACB=45”ć£¬
”ą”ĻABC=45”ć£®
ÓÉÕż·½ŠĪADEFµĆAD=AF£¬
”ß”ĻDAF=”ĻBAC=90”ć£¬
”ą”ĻDAB=”ĻFAC£¬
”ą”÷DAB”Õ”÷FAC£ØSAS£©£¬
”ą”ĻACF=”ĻABD£®
”ą”ĻBCF=”ĻACB+”ĻACF=90”ć£®
¼“CF”ĶBD£®
£Ø2£©AB”ŁACŹ±£¬CF”ĶBDµÄ½įĀŪ³ÉĮ¢£®
ĄķÓÉŹĒ£ŗ
¹żµćA×÷GA”ĶAC½»BCÓŚµćG£¬
”ß”ĻACB=45”ć£¬
”ą”ĻAGD=45”ć£¬
”ąAC=AG£¬
Ķ¬ĄķæÉÖ¤£ŗ”÷GAD”Õ”÷CAF
”ą”ĻACF=”ĻAGD=45”ć£¬”ĻBCF=”ĻACB+”ĻACF=90”ć£¬
¼“CF”ĶBD£®
£Ø3£©¹żµćA×÷AQ”ĶBC½»CBµÄŃÓ³¤ĻßÓŚµćQ£¬
¢ŁµćDŌŚĻ߶ĪBCÉĻŌĖ¶ÆŹ±£¬
”ß”ĻBCA=45”ć£¬æÉĒó³öAQ=CQ=4£®
”ąDQ=4©x£¬”÷AQD”×”÷DCP£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £®
£®
¢ŚµćDŌŚĻ߶ĪBCŃÓ³¤ĻßÉĻŌĖ¶ÆŹ±£¬
”ß”ĻBCA=45”ć£¬
”ąAQ=CQ=4£¬
”ąDQ=4+x£®
¹żA×÷AQ”ĶBC£¬
”ą”ĻQ=”ĻFAD=90”ć£¬
”ß”ĻC”äAF=”ĻC”äCD=90”ć£¬”ĻAC”äF=”ĻCC”äD£¬
”ą”ĻADQ=”ĻAFC”䣬
Ōņ”÷AQD”×”÷AC”äF£®
”ąCF”ĶBD£¬
”ą”÷AQD”×”÷DCP£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £®
£®


 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪ![]() ÖŠ£¬¶Ō½ĒĻß
ÖŠ£¬¶Ō½ĒĻß![]() µÄ“¹Ö±Ę½·ÖĻß
µÄ“¹Ö±Ę½·ÖĻß![]() Óė
Óė![]() Ļą½»ÓŚµć
Ļą½»ÓŚµć![]() £¬Óė
£¬Óė![]() Ļą½»ÓŚµć
Ļą½»ÓŚµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() ”£
ӣ

£Ø1£©ĒóÖ¤£ŗĖıߊĪ![]() ŹĒĮāŠĪ£»
ŹĒĮāŠĪ£»
£Ø2£©Čō![]() £¬Ēó
£¬Ēó![]() µÄ³¤”£
µÄ³¤”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
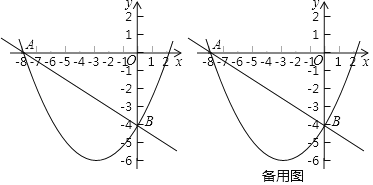
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻßy£½ax2+bx©4¾¹żµćA£Ø©8£¬0£©£¬¶Ō³ĘÖįŹĒÖ±Ļßx£½©3£¬µćBŹĒÅ×ĪļĻßÓėyÖį½»µć£¬µćM”¢NĶ¬Ź±“ÓŌµćO³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶Č·Ö±šŃŲxÖįµÄøŗ°ėÖį”¢yµÄøŗ°ėÖį·½ĻņŌČĖŁŌĖ¶Æ£¬£Øµ±µćNµ½“ļµćBŹ±£¬µćM”¢NĶ¬Ź±Ķ£Ö¹ŌĖ¶Æ£©£®¹żµćM×÷xÖįµÄ“¹Ļߣ¬½»Ö±ĻßABÓŚµćC£¬Į¬½ÓCN”¢MN£¬²¢×÷”÷CMN¹ŲÓŚÖ±ĻßMCµÄ¶Ō³ĘĶ¼ŠĪ£¬µĆµ½”÷CMD£®ÉčµćNŌĖ¶ÆµÄŹ±¼äĪŖtĆė£¬”÷CMDÓė”÷AOBÖŲµž²æ·ÖµÄĆ껿ĪŖS£®
£Ø1£©ĒóÅ×ĪļĻßµÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©µ±0£¼t£¼2Ź±£¬
¢ŁĒóSÓėtµÄŗÆŹż¹ŲĻµŹ½.
¢ŚÖ±½ÓŠ“³öµ±t£½_____Ź±£¬ĖıߊĪCDMNĪŖÕż·½ŠĪ.
£Ø3£©µ±µćDĀäŌŚ±ßABÉĻŹ±£¬¹żµćC×÷Ö±ĻßEF½»Å×ĪļĻßÓŚµćE£¬½»xÖįÓŚµćF£¬Į¬½ÓEB£¬µ±S”÷CBE£ŗS”÷ACF£½1£ŗ3Ź±£¬Ö±½ÓŠ“³öµćEµÄ×ų±źĪŖ______£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»Į¾“ÓAÕ¾æŖĶłDÕ¾µÄ¶Æ³µ£¬Ķ¾ÖŠ¾Ķ£B”¢CĮ½Õ¾£¬»„²»ĻąŹ¶µÄ¼×”¢ŅŅ”¢±ūČżČĖĶ¬Ź±“ÓAÕ¾ÉĻ³µ”£
£Ø1£©Ēó¼×”¢ŅŅĮ½ČĖŌŚĶ¬Ņ»³µÕ¾ĻĀ³µµÄøÅĀŹ£»
£Ø2£©¼×”¢ŅŅ”¢±ūČżČĖŌŚĶ¬Ņ»³µÕ¾ĻĀ³µµÄøÅĀŹĪŖ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚxÖįµÄÕż°ėÖįÉĻŅĄ“Ī¼äøōĻąµČµÄ¾ąĄėČ”µćA1£¬A2£¬A3£¬A4£¬”£¬An£¬·Ö±š¹żÕāŠ©µć×öxÖįµÄ“¹ĻßÓė·“±ČĄżŗÆŹży£½![]() µÄĶ¼ĻóĻą½»ÓŚµćP1£¬P2£¬P3£¬P4£¬”Pn£¬ŌŁ·Ö±š¹żP2£¬P3£¬P4£¬”Pn×÷P2B1”ĶA1P1£¬P3B2”ĶA2P2£¬P4B3”ĶA3P3£¬”£¬PnBn©1”ĶAn©1Pn©1£¬“¹×ć·Ö±šĪŖB1£¬B2£¬B3£¬B4£¬”£¬Bn©1£¬Į¬½ÓP1P2£¬P2P3£¬P3P4£¬”£¬Pn©1Pn£¬µĆµ½Ņ»×éRt”÷P1B1P2£¬Rt”÷P2B2P3£¬Rt”÷P3B3P4£¬”£¬Rt”÷Pn©1Bn©1Pn£¬ŌņRt”÷Pn©1Bn©1PnµÄĆ껿ĪŖ_____£®
µÄĶ¼ĻóĻą½»ÓŚµćP1£¬P2£¬P3£¬P4£¬”Pn£¬ŌŁ·Ö±š¹żP2£¬P3£¬P4£¬”Pn×÷P2B1”ĶA1P1£¬P3B2”ĶA2P2£¬P4B3”ĶA3P3£¬”£¬PnBn©1”ĶAn©1Pn©1£¬“¹×ć·Ö±šĪŖB1£¬B2£¬B3£¬B4£¬”£¬Bn©1£¬Į¬½ÓP1P2£¬P2P3£¬P3P4£¬”£¬Pn©1Pn£¬µĆµ½Ņ»×éRt”÷P1B1P2£¬Rt”÷P2B2P3£¬Rt”÷P3B3P4£¬”£¬Rt”÷Pn©1Bn©1Pn£¬ŌņRt”÷Pn©1Bn©1PnµÄĆ껿ĪŖ_____£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ć껿ĪŖ1µÄµČŃüÖ±½Ē”÷OA1A2£¬”ĻOA2A1=90”ć£¬ĒŅOA2ĪŖŠ±±ßŌŚ”÷OA1A2Ķā×÷µČŃüÖ±½Ē”÷OA2A3£¬ŅŌOA3ĪŖŠ±±ßŌŚ”÷OA2A3Ķā×÷µČŃüÖ±½Ē”÷OA3A4£¬ŅŌOA4ĪŖŠ±±ßŌŚ”÷OA3A4Ķā×÷µČŃüÖ±½Ē”÷OA4A5£¬”Į¬½ÓA1A3£¬A3A5£¬A5A7£¬”·Ö±šÓėOA2£¬OA4£¬OA6£¬”½»ÓŚµćB1£¬B2£¬B3£¬”°““Ė¹ęĀɼĢŠųĻĀČ„£¬¼Ē”÷OB1A3µÄĆ껿ĪŖS1£¬”÷OB2A5µÄĆ껿ĪŖS2£¬”÷OB3A7µÄĆ껿ĪŖS3£¬””÷OBnA2n+1µÄĆ껿ĪŖSn£¬ŌņSn=__£ØÓĆŗ¬ÕżÕūŹżnµÄŹ½×Ó±ķŹ¾£©£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
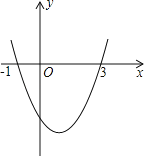
”¾ĢāÄæ”æŅŃÖŖ¶ž“ĪŗÆŹży£½ax2+bx+cµÄĶ¼ĻóČēĶ¼ĖłŹ¾£¬ĖüÓėxÖįµÄĮ½øö½»µćµÄ×ų±ź·Ö±šĪŖ(©1£¬0)£¬(3£¬0)£¬ĒŅµćP1(x1£¬y1)”¢P2(x2£¬y2)ŌŚ“ĖÅ×ĪļĻßÉĻ£®¶ŌÓŚĻĀĮŠ½įĀŪ£ŗ¢Łabc£¾0£»¢Śb2©4ac£¾0£»¢Ūµ±x1£¼x2£¼0Ź±£¬y1£¾y2£»¢Üµ±©1£¼x£¼3Ź±£¬y£¼0£®ĘäÖŠÕżČ·µÄŹĒ_____(ĢīŠņŗÅ)
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚŅ»øö²»ĶøĆ÷µÄæŚ“ü֊װӊ3øö“ųŗÅĀėµÄĒņ£¬ĒņŗÅ·Ö±šĪŖ2£¬3£¬4£¬ÕāŠ©Ēņ³żŗÅĀė²»Ķ¬ĶāĘäĖü¾łĻąĶ¬”£¼×”¢ŅŅ”¢Į½Ķ¬Ń§ĶęĆžĒņÓĪĻ·£¬ÓĪĻ·¹ęŌņČēĻĀ£ŗ
ĻČÓɼ×Ķ¬Ń§“ÓÖŠĖ껜ƞ³öŅ»Ēņ£¬¼ĒĻĀĒņŗÅ£¬²¢·Å»Ų½ĮŌČ£¬ŌŁÓÉŅŅĶ¬Ń§“ÓÖŠĖ껜ƞ³öŅ»Ēņ£¬¼ĒĻĀĒņŗÅ”£½«¼×Ķ¬Ń§Ćž³öµÄĒņŗÅ×÷ĪŖŅ»øöĮ½Ī»ŹżµÄŹ®Ī»ÉĻµÄŹż£¬ŅŅĶ¬Ń§µÄ×÷ĪŖøöĪ»ÉĻµÄŹż”£ČōøĆĮ½Ī»ŹżÄܱ»4Õū³ż£¬Ōņ¼×Ź¤£¬·ńŌņŅŅŹ¤.
ĪŹ£ŗÕāøöÓĪĻ·¹«Ę½Āš£æĒėĖµĆ÷ĄķÓÉ”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬ŌŚ¾ŲŠĪ![]() ÖŠ£¬
ÖŠ£¬![]() ŹĒ¶Ō½ĒĻߣ¬µć
ŹĒ¶Ō½ĒĻߣ¬µć![]() ĪŖ¾ŲŠĪĶāŅ»µćĒŅĀś×ć
ĪŖ¾ŲŠĪĶāŅ»µćĒŅĀś×ć![]() £¬
£¬![]() £¬
£¬![]() ½»
½»![]() ÓŚµć
ÓŚµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ½»
½»![]() ÓŚ
ÓŚ![]() £®
£®
£Ø1£©Čō![]() £¬
£¬![]() £¬Ēó¾ŲŠĪ
£¬Ēó¾ŲŠĪ![]() µÄĆ껿£»
µÄĆ껿£»
£Ø2£©Čō![]() £¬ŹŌÅŠ¶ĻĻ߶Ī
£¬ŹŌÅŠ¶ĻĻ߶Ī![]() ”¢
Ӣ![]() Ӣ
”¢![]() Ö®¼äµÄ¹ŲĻµ£¬²¢Ö¤Ć÷£®
Ö®¼äµÄ¹ŲĻµ£¬²¢Ö¤Ć÷£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com