
【题目】阅读材料:我们知道,4x+2x-x=(4+2-1)x=5x,类似地,我们把(a+b)看成一个整体,则4(a+b)+2(a+b)-(a+b)-(4+2-1)(a+b)=5(a+b).“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.
尝试应用:
(1)把(a-b)看成一个整体,合并3(a-b)2-7(a-b)2+2(a-b)2的结果是____________.
(2)已知x2-2y=5,求21-![]() x2+y的值;
x2+y的值;
(3)拓广探索:已知a-2b=3,2b-c=-5,c-d=10,求2(a-c)+2(2b-d)-2(2b-c)的值.
【答案】(1) -2(a-b)2;(2)18![]() ;(3)16.
;(3)16.
【解析】
(1)把(ab)看做一个整体,合并即可得到结果;
(2)把(x2-2y)整体代入即可求解;
(3)原式去括号整理后,将已知等式代入计算即可求出值.
解:(1)3(a-b)2-7(a-b)2+2(a-b)2= -2(a-b)2
故答案为:-2(a-b)2;
(2)∵x2-2y=5
∴21-![]() x2+y =21-
x2+y =21-![]() (x2-2y)=21-
(x2-2y)=21-![]() =18
=18![]()
(3)∵a-2b=3,2b-c=-5,c-d=10
∴2(a-c)+2(2b-d)-2(2b-c)
= 2a - 2c + 4b - 2d - 4b + 2c
=(2a-4b)+(4b-2c)+(2c-2d)
= 2×3 +2×(-5)+2×10
= 16


科目:初中数学 来源: 题型:
【题目】如图,粗线A→C→B和细线A→D→E→F→G→H→B是公交车从少年宫A到体育馆B的两条行驶路线.
(1)判断两条线路的长短;
(2)小丽坐出租车由体育馆B到少年宫A,假设出租车的收费标准为:起步价为7元,3千米以后每千米1.8元,用代数式表示出租车的收费m元与行驶路程s(s>3)千米之间的关系;
(3)如果这段路程长4.5千米,小丽身上有10元钱,够不够小丽坐出租车由体育馆到少年宫呢?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
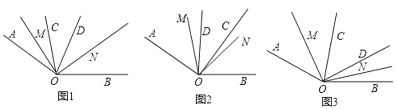
【题目】已知∠AOB=α(90°<α<180°),∠COD在∠AOB的内部,OM平分∠AOC,ON平分∠BOD.
(1)若∠COD=180°-α时,探索下面两个问题:
①如图1,当OC在OD左侧,求∠MON的度数;
②当OC在OD右侧,请在图2内补全图形,并求出∠MON的度数(用含α的代数式表示);
(2)如图3,当∠COD=kα,且CO在OD左侧时,直接写出∠MON的度数(用含α,k的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC.
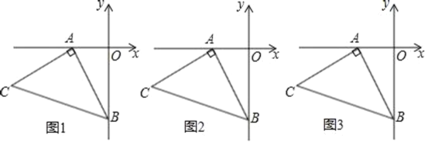
(1)求C点的坐标;
(2)如图1,在平面内是否存在一点H,使得以A、C、B、H为顶点的四边形为平行四边形?若存在,请直接写出H点坐标;若不存在,请说明理由;
(3)如图1点M(1,﹣1)是第四象限内的一点,在y轴上是否存在一点F,使得|FM﹣FC|的值最大?若存在,请求出F点坐标;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并解决有关问题:我们知道|x|=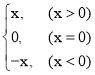 ,现在我们可以用这个结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别叫做|x+1|与|x﹣2|的零点值.)在有理数范围内,零点值x=﹣1和x=2可将全体有理数分成不重复且不遗漏的如下3种情况:
,现在我们可以用这个结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别叫做|x+1|与|x﹣2|的零点值.)在有理数范围内,零点值x=﹣1和x=2可将全体有理数分成不重复且不遗漏的如下3种情况:
(1)当x<﹣1时,原式=﹣(x+1)﹣(x﹣2)=﹣2x+1;
(2)当﹣1≤x≤2时,原式=x+1﹣(x﹣2)=3;
(3)当x>2时,原式=x+1+x﹣2=2x﹣1.
综上所述,原式=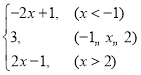 .
.
通过以上阅读,请你解决以下问题:
(1)分别求出|x+2|和|x﹣4|的零点值;
(2)化简代数式|x+2|+|x﹣4|;
(3)求方程:|x+2|+|x﹣4|=6的整数解;
(4)|x+2|+|x﹣4|是否有最小值?如果有,请直接写出最小值;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年周杰伦地表最强巡回演唱会于11月17日在贵阳奥林匹克体育中心举行,小颖购买了一张票价为四位数的场地票(动感地带专属),而小明一张购买了票价为三位数的看台票(动感地带专属)。小颖说,“在你的票价前面多写个1,都还比我的便宜200元”;小明说,“只需在我的票价后多写个0,就比你的贵3120元”.请问小颖和小明购买的演唱会门票各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家商场平时以同样价格出售相同的商品,春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中超过200元后的价格部分打7折.
(1)以x(单位:元)表示商品原价,y(单位:元)表示购物金额,分别就两家商场的让利方式写出y关于x的函数解析式;
(2)在同一直角坐标系中画出(1)中函数的图象;
(3)春节期间如何选择这两家商场去购物更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将口ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF
(2)若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
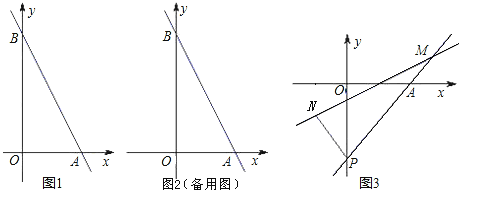
【题目】如图1,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(2,0), B(0,4).
(1)求直线AB的解析式;
(2)若点M为直线y=mx在第一象限上一点,且△ABM是等腰直角三角形,求m的值.
(3)如图3,过点A(2,0)的直线![]() 交y轴负半轴于点P,N点的横坐标为-1,过N点的直线
交y轴负半轴于点P,N点的横坐标为-1,过N点的直线![]() 交AP于点M.求
交AP于点M.求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com