
【题目】某商场试销一种成本为每件120元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量![]() (件)是销售单价
(件)是销售单价![]() (元)的函数,并且满足如下对应值表:
(元)的函数,并且满足如下对应值表:
销售单价 | 130 | 140 | 145 |
销售量 | 110 | 100 | 95 |
(1)求![]() 与
与![]() 的函数表达式;
的函数表达式;
(2)若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于 2000元,试确定销售单价![]() 的范围.
的范围.
【答案】(1)![]() ;(2)
;(2)![]() ,定价为174元时,利润最大为3564元;(3)
,定价为174元时,利润最大为3564元;(3)![]() .
.
【解析】试题分析: (1)列出二元一次方程组解出k与b的值可求出一次函数的表达式.
(2)依题意求出W与x的函数表达式可推出当x=174时商场可获得最大利润.
(3)由w=2000推出x300x+16400=0x2-180x+7700=0解出x的值即可.
试题解析:
(1)根据题意得![]()
解得k=1,b=240.
所求一次函数的表达式为y=x+240.
(2)W=(x120)(x+240)=x+360x28800=(x180) +3600,
∵抛物线的开口向下,
∴当x<150时,W随x的增大而增大,
而销售单价不低于成本单价,且获利不得高于45%,
即120x120×(1+45%),
∴120x174,
∴当x=174时,W=(174180) +3600=3564.
∴当销售单价定为174元时,商场可获得最大利润,最大利润是3564元.
(3)由W2000,得2000(x180) +3600,
整理得,x360x+308000,
而方程x360x+30800=0的解为x =140,x =220.
即x =140,x =220时利润为2000元,而函数y= x360x+30800的开口向下,所以要使该商场获得利润不低于2000元,销售单价应在140元到220元之间,
而120元/件x174元/件,所以,销售单价x的范围是140元/件x174元/件。


科目:初中数学 来源: 题型:
【题目】某中学九(1)班6个同学在课间体育活动时进行1分钟跳绳比赛,成绩如下:126,144,134,118,126,152.这组数据中,众数和中位数分别是( )
A.126,126
B.130,134
C.126,130
D.118,152
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC放置在平面直角坐标系中,已知A(0,0)、B(2,0),反比例函数的图象经过点C.
(1)求点C的坐标及反比例函数的解析式.
(2)如果将等边△ABC向上平移n个单位长度,使点B恰好落在双曲线上,求n的值.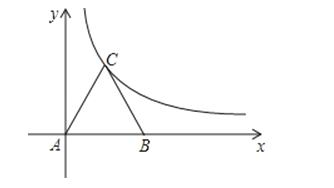
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将多项式4a2b+2b3﹣3ab2﹣a3按字母b的降幂排列正确的是( )
A.4a2b﹣3ab2+2b3﹣a3
B.﹣a3+4a2b﹣3ab2+2b3
C.﹣3ab2+4a2b﹣a3+2b3
D.2b3﹣3ab2+4a2b﹣a3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com